题目内容
5.已知二次函数f(x)=ax2+bx+c(a≠0).(1)若f(-1)=0,试判断函数f(x)的零点个数;
(2)若对任意的x1,x2 ∈R.且x1<x2 ,f(x1)≠f(x2),试证明存在x0∈(x1,x2 ),使得f(x0)=$\frac{1}{2}$[f(x1)+f(x2)]成立.
分析 (1)由f(-1)=0可求得b=a+c,利用△=(a-c)2分析判断即可;
(2)令g(x)=f(x)-$\frac{1}{2}$[f(x1)+f(x2)],可证得g(x1)g(x2)<0,由零点存在定理可知存在x0∈(x1,x2),使f(x0)=$\frac{1}{2}$[f(x1)+f(x2)]成立.
解答 (1)解:∵f(-1)=0,
∴a-b+c=0,则b=a+c,
∵△=b2-4ac=(a-c)2,
∴当a=c时,△=0,此函数f(x)有一个零点;
当a≠c时,△>0.函数f(x)有两个零点.
(2)证明:令g(x)=f(x)-$\frac{1}{2}$[f(x1)+f(x2)],则
g(x1)=f(x1)-$\frac{1}{2}$[f(x1)+f(x2)]
=$\frac{1}{2}$[f(x1)-f(x2)]g(x2)
=f(x2)-$\frac{1}{2}$[f(x1)+f(x2)]
=$\frac{1}{2}${f(x2)-f(x1)},
∵f(x1)≠f(x2)
∴g(x1)g(x2)<0,所以g(x)=0在(x1,x2)内必有一个实根,
即存在x0∈(x1,x2)使f(x0)=$\frac{1}{2}$[f(x1)+f(x2)]成立.
点评 本题考查二次函数的性质,考查函数零点的判定定理,考查化归思想与构造函数的思想的综合应用,属于难题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.用五点法画函数f(x)=2sin2x在长度为一个周期的闭区间上的简图.
| x | |||||
| 2x | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| f(x)=2sin2x |
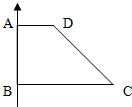 如图1,直角梯形ABCD中,∠A=∠B=90°,AD∥BC,AD=2,AB=3,BC=6,把直角梯形ABCD绕边AB旋转一周得到一个旋转体,求:
如图1,直角梯形ABCD中,∠A=∠B=90°,AD∥BC,AD=2,AB=3,BC=6,把直角梯形ABCD绕边AB旋转一周得到一个旋转体,求: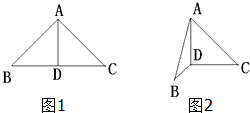 已知Rt△ABC中,AB=AC=a,AD是斜边BC上的高,以AD为折痕使∠BDC成直角,
已知Rt△ABC中,AB=AC=a,AD是斜边BC上的高,以AD为折痕使∠BDC成直角,