Question

【题目】已知f（x）=ex﹣ax2﹣2x+b（e为自然对数的底数，a，b∈R）．
（Ⅰ）设f′（x）为f（x）的导函数，证明：当a＞0时，f′（x）的最小值小于0；
（Ⅱ）若a＜0，f（x）＞0恒成立，求符合条件的最小整数b．

Answer 1

【答案】解：（Ⅰ）证明：令g（x）=f'（x）=ex﹣2ax﹣2，则g'（x）=ex﹣2a，
因为a＞0，令g'（x0）=0，x0=ln2a，
所以当x∈（﹣∞，ln2a）时，g'（x）＜0，g（x）单调递减；
当x∈（ln2a，+∞）时，g'（x）＞0，g（x）单调递增
则f'（x）min=g（x）min=g（ln2a）=eln2a﹣2aln2a﹣2=2a﹣2aln2a﹣2
令G（x）=x﹣xlnx﹣2，（x＞0）G'（x）=1﹣（lnx+1）=﹣lnx当x∈（0，1）时，
G'（x）＞0，G（x）单调递增
当x∈（1，+∞）时，G'（x）＜0，G（x）单调递减
所以G（x）max=G（1）=﹣1＜0，所以f'（x）min＜0成立．
（Ⅱ）f（x）＞0恒成立，等价于f（x）min＞0恒成立
令g（x）=f'（x）=ex﹣2ax﹣2，则g'（x）=ex﹣2a，
因为a＜0，所以g'（x）＞0，所以g（x）单调递增，
又g（0）=﹣1＜0，g（1）=e﹣2a﹣2＞0，所以存在x0∈（0，1），使得g（x0）=0
则x∈（﹣∞，x0）时，g（x）=f'（x）＜0，f（x）单调递减；
x∈（x0 ， +∞）时，g（x）=f'（x）＞0，f（x）单调递增；
所以f（x）min=f（x0）=ex0﹣ax02﹣2x0+b＞0恒成立…（1）
且ex0﹣2ax0﹣2=0…（2）
由（1）（2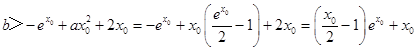）， 即可
又由（2）a= ＜0，所以x0∈（0，ln2）
令 +x，x∈（0，ln2）n（x）=m'（x）= +1n'（x）= ＞0，
所以n（x）＞n（0）= ＞0，所以m（x）单调递增，m（x）＞m（0）=（﹣1）e0=﹣1， +ln2=2ln2﹣2
所以b＞﹣1，所以符合条件的b=0
法2：令x=0，f（0）=1+b＞0，b＞﹣1，故符合条件的最小整数b=0．
现证明b=0时，f（x）＞0 求f（x）=ex﹣ax2﹣2x的最小值即可
令g（x）=f'（x）=ex﹣2ax﹣2，则g'（x）=ex﹣2a，因为a＜0，所以g'（x）＞0，所以g（x）单调递增，
又g（0）=﹣1＜0，g（1）=e﹣2a﹣2＞0，所以存在x0∈（0，1），使得g（x0）=0，
则x∈（﹣∞，x0）时，g（x）=f'（x）＜0，f（x）单调递减；
x∈（x0 ， +∞）时，g（x）=f'（x）＞0，f（x）单调递增；
所以f（x）min=f（x0）=ex0﹣ax02﹣2x0 ． （1）
且ex0﹣2ax0﹣2=0…（2）
f（x）min=f（x0）=ex0﹣
又由（2）a= ＜0，所以x0∈（0，ln2））
现在求函数 ﹣x，x∈（0，ln2）的范围q（x0）=p'（x）= ﹣1，q'（x0）=﹣ ＜0，
所以q（x）＜q（0）=﹣ ＜0，所以p（x）单调递减，p（x）＜p（0）=（﹣1）e0=1 ﹣ln2=2﹣ln2＞0
所以b=0是符合条件的．
【解析】（Ⅰ）令g（x）=f'（x）=ex﹣2ax﹣2，求出g'（x）=ex﹣2a，判断导函数的符号，推出单调性，求出原函数的导数的最小值，再构造最小值函数，利用导数求解最小值函数的最大值为负值，说明f'（x）min＜0成立．（Ⅱ）利用f（x）＞0恒成立，等价于f（x）min＞0恒成立，构造g（x）=f'（x）=ex﹣2ax﹣2，求出导函数g'（x）=ex﹣2a，判断单调性，推出 恒成立且 求出b的表达式，a的表达式，在构造函数令 ，判断单调性，求出满足椭圆的b即可．法2：令x=0，得到符合条件的最小整数b=0，然后证明b=0时，f（x）＞0 求f（x）=ex﹣ax2﹣2x的最小值．令g（x）=f'（x）=ex﹣2ax﹣2，判断g（x）单调性，求解函数 ，且 ，在构造函数函数 ，利用函数的最值，推出b=0是符合条件的．