题目内容
【题目】已知数列![]() 满足
满足![]() ,对每个正整数
,对每个正整数![]() ,有
,有![]() 或
或![]() .如这个数列可以为1,2,4,6,10….
.如这个数列可以为1,2,4,6,10….
(1)若某一项![]() 为奇数,且不为3的倍数,证明:
为奇数,且不为3的倍数,证明:![]() ;
;
(2)证明: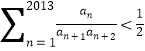 ;
;
(3)若在![]() 的前2015项中,恰有t个项为奇数,求t的最大值.
的前2015项中,恰有t个项为奇数,求t的最大值.
【答案】(1)见解析;(2)见解析;(3)1343
【解析】
(1)由am不为偶数,知![]() .
.
于是,![]() .
.
假如![]() ,则
,则![]() 为3的倍数,与已知条件矛盾.
为3的倍数,与已知条件矛盾.
从而,只能是![]() .
.
故![]() .
.
(2)由递推关系,易知数列![]() 是单调递增的.
是单调递增的.
因此,当![]() 时,
时,![]() .
.
从而,![]() ,即
,即![]() .
.
由此,![]() .
.
故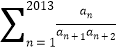
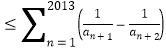
![]()
(3)一方面,数列![]() 的任意相邻三项至多有两个奇数.
的任意相邻三项至多有两个奇数.
事实上,假如![]() 均为奇数,由
均为奇数,由![]() 均为偶数,故根据递推关系知
均为偶数,故根据递推关系知![]() 为偶数,矛盾.
为偶数,矛盾.
因此,在![]() 这671组数中,每组至多含两个奇数.
这671组数中,每组至多含两个奇数.
再考虑到![]() 为奇数,
为奇数,![]() 为偶数,故至多有
为偶数,故至多有![]() 个奇数,即
个奇数,即![]() .
.
另一方面 ,当数列![]() 总满足
总满足![]() 时,注意到,
时,注意到,![]() 为奇数,
为奇数,![]() 为偶数,故对每个正整数k,由递推关系得
为偶数,故对每个正整数k,由递推关系得![]() 为奇数,
为奇数,![]() 为奇数,
为奇数,![]() 为偶数,此时,数列
为偶数,此时,数列![]() 的前2015项含有1343个奇数.
的前2015项含有1343个奇数.
综上,t的最大值1343.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目