[题目]某学校青年职工.中年职工.老年职工的人数之比为7:5:3.为了了解该单位职工的健康情况.用分层抽样的方法从中抽取样本．若样本中的青年职工为14人.则样本容量为．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】某学校青年职工、中年职工、老年职工的人数之比为7:5:3，为了了解该单位职工的健康情况，用分层抽样的方法从中抽取样本．若样本中的青年职工为14人，则样本容量为______．

【答案】30

【解析】

根据给出的单位青年职工、中年职工、老年职工的人数之比为7：5：3，得到青年职工在单位所占的人数比例，从而得到中年职工和老年职工的人数和所占的比例，运用分层抽样中每层所抽取的比例相等，求该单位中年职工和老年职工被抽取的人数和．

因为单位中青年职工、中年职工、老年职工的人数之比为7：5：3，所以青年职工所占人数比例为，

中年职工与老年职工的和所占人数比例为，

设样本中中年职工和老年职工的人数和为m，

则所以m=16，所以样本容量为14+16=30．

故答案为：30.

练习册系列答案

名校课堂系列答案

相关题目

【题目】已知A，B是椭圆 =1和双曲线 =1的公共顶点，其中a＞b＞0，P是双曲线上的动点，M是椭圆上的动点（P，M都异于A，B），且满足 =λ（）（λ∈R），设直线AP，BP，AM，BM的斜率分别为k1 ， k2 ， k3 ， k4 ，若k1+k2= ，则k3+k4= ．

【题目】若方程|x2﹣2x﹣1|﹣t=0有四个不同的实数根x1、x2、x3、x4，且x1＜x2＜x3＜x4 ，则2（x4﹣x1）+（x3﹣x2）的取值范围是（）
A.（8，6 ）
B.（6 ，4 ）
C.[8，4 ]
D.（8，4 ]

【题目】在极坐标系中，圆的方程为，以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的参数方程为（为参数）

（1）求圆的直角坐标方程和直线的普通方程；

（2）若直线与圆相切，求实数的值；

【题目】全世界越来越关注环境保护问题，某监测站点于2018年1月某日起连续天监测空气质量指数()，数据统计如下：

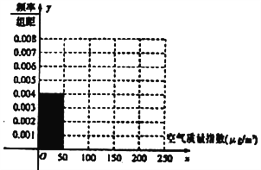
（1）根据所给统计表和频率分布直方图中的信息求出，的值，并完成频率分布直方图；

（2）由频率分布直方图，求该组数据的众数和中位数；

（3）在空气质量指数分别属于和的监测数据中，用分层抽样的方法抽取天，再从中任意选取天，求事件“两天空气都为良”发生的概率.

【题目】已知函数f（x）=|cosx|sinx，给出下列五个说法：
①f（ π）=﹣ ；
②若|f（x1）|=|f（x2）|，则x1=x2+kπ（k∈Z）；
③f（x）在区间[﹣ ， ]上单调递增；
④函数f（x）的周期为π．
⑤f（x）的图象关于点（，0）成中心对称．
其中正确说法的序号是．

【题目】如图，在四棱锥中，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，AB⊥AD，AB=1，AD=2， .

（1）求证：PD⊥平面PAB；

（2）求直线PB与平面PCD所成角的正弦值.

日车流量x	0≤x＜5	5≤x＜10	10≤x＜15	15≤x＜20	20≤x＜25	x≥25
频率	0.05	0.25	0.35	0.25	0.10	0

将日车流量落入各组的频率视为概率，并假设每天的车流量相互独立．
（1）求在未来连续3天里，有连续2天的日车流量都不低于10万辆且另1天的日车流量低于5万辆的概率；
（2）用X表示在未来3天时间里日车流量不低于10万辆的天数，求X的分布列和数学期望．

试题分类