题目内容
【题目】已知函数f(x)=|cosx|sinx,给出下列五个说法:
①f( ![]() π)=﹣
π)=﹣ ![]() ;
;
②若|f(x1)|=|f(x2)|,则x1=x2+kπ(k∈Z);
③f(x)在区间[﹣ ![]() ,
, ![]() ]上单调递增;
]上单调递增;
④函数f(x)的周期为π.
⑤f(x)的图象关于点( ![]() ,0)成中心对称.
,0)成中心对称.
其中正确说法的序号是 .
【答案】①③
【解析】解:由题意函数f(x)=|cosx|sinx= 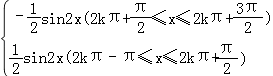 (k∈Z);
(k∈Z);
对于①:f( ![]() π)=|cos
π)=|cos ![]() |sin
|sin ![]() =)=|cos(
=)=|cos( ![]() )|sin(27π
)|sin(27π ![]() )=
)= ![]() =﹣
=﹣ ![]() ;所以①对
;所以①对
对于②:若|f(x1)|=|f(x2)|,当x2= ![]() ,x1=
,x1= ![]() 时,成立,则x1=x2+
时,成立,则x1=x2+ ![]() ,所以②不对
,所以②不对
对于③f(x)在区间[﹣ ![]() ,
, ![]() ]上时,f(x)=
]上时,f(x)= ![]() sin2x,可得2x∈[-
sin2x,可得2x∈[- ![]() ,
, ![]() ],x∈[﹣
],x∈[﹣ ![]() ,
, ![]() ]上是单调递增;所以③对.
]上是单调递增;所以③对.
对于④:函数f(x)=|cosx|sinx,则f(x+π)=|cos(x+π)|sin(x+π)=﹣(|cosx|sinx)=﹣f(x),可得函数f(x)的周期不是π.所以④不对.
对于⑤:由于f( ![]() )=|cos(x+
)=|cos(x+ ![]() )|sin(x+
)|sin(x+ ![]() )=cosx|sinx|,f(
)=cosx|sinx|,f( ![]() )=|cos(﹣x+
)=|cos(﹣x+ ![]() )|sin(﹣x+
)|sin(﹣x+ ![]() )=cosx|sinx|
)=cosx|sinx|
则:f( ![]() )=f(
)=f( ![]() )图象关于x=
)图象关于x= ![]() 对称.所以⑤不对.
对称.所以⑤不对.
综上所得:①③正确,②④⑤不对.
所以答案是:①③.

 阅读快车系列答案
阅读快车系列答案【题目】北京市环境保护监测中心每月向公众公布北京市各区域的空气质量状况![]() 年1月份各区域的
年1月份各区域的![]() 浓度情况如表:
浓度情况如表:
各区域1月份![]() 浓度
浓度![]() 单位:微克
单位:微克![]() 立方米
立方米![]() 表
表
区域 |
| 区域 |
| 区域 |
|
怀柔 | 27 | 海淀 | 34 | 平谷 | 40 |
密云 | 31 | 延庆 | 35 | 丰台 | 42 |
门头沟 | 32 | 西城 | 35 | 大兴 | 46 |
顺义 | 32 | 东城 | 36 | 开发区 | 46 |
昌平 | 32 | 石景山 | 37 | 房山 | 47 |
朝阳 | 34 | 通州 | 39 |
从上述表格随机选择一个区域,其2018年1月份![]() 的浓度小于36微克
的浓度小于36微克![]() 立方米的概率是
立方米的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()