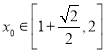题目内容
【题目】在下列命题中:①在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则解三角形只有唯一解的充要条件是:
,则解三角形只有唯一解的充要条件是:![]() ;②当
;②当![]() 时,
时,![]() ;③在
;③在![]() 中,若
中,若![]() ,则
,则![]() 中一定为钝角三角形;④扇形圆心角
中一定为钝角三角形;④扇形圆心角![]() 为锐角,周长为定值,则它面积最大时,一定有
为锐角,周长为定值,则它面积最大时,一定有![]() ;⑤函数
;⑤函数![]() 的单增区间为
的单增区间为![]() ,其中真命题的序号为_____.
,其中真命题的序号为_____.
【答案】①②③⑤;
【解析】
对每一个命题逐一分析判断得解. ①,利用正弦定理分析判断;②,利用反三角函数的图象分析判断;③,利用反证法判断;④,利用基本不等式判断得解;⑤,利用复合函数的单调性分析求解.
①,由正弦定理得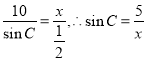 ,因为三角形有唯一解,所以
,因为三角形有唯一解,所以![]() 或
或![]() ,所以该命题正确;
,所以该命题正确;
②,画图得

当![]() 时,
时,![]() ,所以该命题是真命题;
,所以该命题是真命题;
③假设△ABC是锐角三角形,![]() ,
,
所以![]() ,显然矛盾;假设△ABC是直角三角形,显然A,B不可能是直角,所以C是直角,此时
,显然矛盾;假设△ABC是直角三角形,显然A,B不可能是直角,所以C是直角,此时![]() ,与已知矛盾,所以
,与已知矛盾,所以![]() 中一定为钝角三角形,所以该命题是真命题;
中一定为钝角三角形,所以该命题是真命题;
④,设扇形的半径为![]() ,扇形圆心角
,扇形圆心角![]() 为锐角,弧长为
为锐角,弧长为![]() ,周长
,周长![]() 为定值,则它面积
为定值,则它面积![]() ,当且仅当
,当且仅当![]() 即
即![]() 时取最大值,但是
时取最大值,但是![]() ,不是锐角,所以该命题不正确;
,不是锐角,所以该命题不正确;
⑤,因为函数![]() 是一个减函数,所以函数
是一个减函数,所以函数![]() 的单增区间为
的单增区间为![]() 的减区间
的减区间![]() ,所以该命题是真命题.
,所以该命题是真命题.
故答案为:①②③⑤

练习册系列答案
相关题目