题目内容
【题目】已知数列![]() ,其前
,其前![]() 项和为
项和为![]() .
.
(1)若对任意的![]() ,
, ![]() ,
, ![]() ,
, ![]() 组成公差为4的等差数列,且
组成公差为4的等差数列,且![]() ,求
,求![]() ;
;
(2)若数列 是公比为
是公比为![]() (
(![]() )的等比数列,
)的等比数列, ![]() 为常数,
为常数,
求证:数列![]() 为等比数列的充要条件为
为等比数列的充要条件为![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)根据题意,可求得![]() ,
, ![]() (
(![]() ),从而得
),从而得![]() ,
, ![]() ,
, ![]() ,……,
,……, ![]() ,
, ![]() 是公差为4的等差数列,且
是公差为4的等差数列,且![]() ,于是可求
,于是可求![]() ;
;
(2)由![]() ,可求得
,可求得![]() ,
,![]() ,两式相减得
,两式相减得![]() ,若
,若![]() ,可证得数列
,可证得数列![]() 为等比数列,(充分性);若数列
为等比数列,(充分性);若数列![]() 为等比数列,可证得
为等比数列,可证得![]() ,(必要性).
,(必要性).
试题解析:(1)因为![]() ,
, ![]() ,
, ![]() 成公差为4的等差数列,
成公差为4的等差数列,
所以![]() ,
, ![]() (
(![]() ),
),
所以![]() ,
, ![]() ,
, ![]() ,……,
,……, ![]() ,
, ![]() 是公差为4的等差数列,且
是公差为4的等差数列,且
![]() ,
,
又因为![]() ,所以
,所以![]()
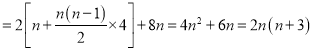
(2)因为![]() ,所以
,所以![]() ,①
,①
所以![]() ,②
,②
②-①,得![]() ,③
,③
(i)充分性:因为![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() ,代入③式,得
,代入③式,得
![]() ,因为
,因为![]() ,又
,又![]() ,
,
所以![]() ,
, ![]() ,所以
,所以![]() 为等比数列,
为等比数列,
(ii)必要性:设![]() 的公比为
的公比为![]() ,则由③得
,则由③得![]() ,
,
整理得![]() ,
,
此式为关于![]() 的恒等式,若
的恒等式,若![]() ,则左边=0,右边=-1,矛盾:
,则左边=0,右边=-1,矛盾:
若![]() ,当且仅当
,当且仅当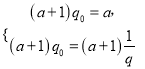 时成立,所以
时成立,所以![]() .
.
由(i)、(ii)可知,数列![]() 为等比数列的充要条件
为等比数列的充要条件![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

