题目内容
9.已知函数f(x)=cos2x+$\sqrt{3}$sinxcosx,x∈R.(1)求f(x)的最小正周期和单调递减区间;
(2)设x=m(m∈R)是函数y=f(x)图象的对称轴,求sin4m的值.
分析 (1)首先通过三角函数的恒等变换,把函数的关系式变性成正弦型函数,进一步求出函数的周期和单调区间.
(2)利用(1)的函数关系式,利用整体思想,用函数的对函数的关系求出结果.
解答 解:(1)f(x)=cos2x+$\sqrt{3}$sinxcosx
=$\frac{1+cos2x}{2}+\frac{\sqrt{3}sin2x}{2}$
=$sin(2x+\frac{π}{6})+\frac{1}{2}$,
所以函数的周期为:$T=\frac{2π}{2}=π$.
令:$\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤$$\frac{3π}{2}+2kπ$(k∈Z),
解得:$kπ+\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$(k∈Z),
所以函数的单调递减区间为:[$kπ+\frac{π}{6}$,$kπ+\frac{2π}{3}$](k∈Z).
(2)设x=m(m∈R)是函数y=f(x)图象的对称轴,
则:$2m+\frac{π}{6}=kπ+\frac{π}{2}$(k∈Z).
解得:m=$\frac{kπ}{2}+\frac{π}{6}$,
所以:4m=2kπ$+\frac{2π}{3}$.
则:sin4m=$\frac{\sqrt{3}}{2}$.
点评 本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的周期和单调性的应用,以及函数的对称轴的应用.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
17.已知集合 A={1,2,m2},B={1,m}.若B⊆A,则m=( )
| A. | 0 | B. | 2 | C. | 0 或2 | D. | 1 或2 |
14.已知实数x,y满足$\left\{\begin{array}{l}2x+y≥0\\ 2x-y≤0\\ 0≤y≤t\end{array}\right.$其中t>0.若z=3x+y的最大值为5,则z的最小值为( )
| A. | $\frac{5}{2}$ | B. | 1 | C. | 0 | D. | -1 |
1.若一个圆锥的正视图(如图所示)是边长为3,3,2的三角形,则该圆锥的表面积是( )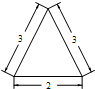

| A. | π | B. | 2π | C. | 3π | D. | 4π |