题目内容
2.设0<α<π,则函数y=sin2α(1-cosα)的最大值为$\frac{32}{27}$.分析 令t=cosα∈(-1,1),可得y=t3-t2-t+1,利用导数y′的符号研究函数的单调性,由单调性求函数y的最大值.
解答 解:函数y=sin2α(1-cosα)=(1-cos2α)(1-cosα)=cos3α-cos2α-cosα+1.
由于0<α<π,可得-1<cosα<1.
令t=cosα∈(-1,1),则y=t3-t2-t+1,∴y′=3t2-2t-1=(3t+1)(t-1).
令y′-0,求得t=-$\frac{1}{3}$,或t=1(舍去).
由y′的符号可得,函数y在(-1,-$\frac{1}{3}$)上是增函数,在(-1,1)上是减函数,
故当t=-$\frac{1}{3}$时,函数y取得最大值为-$\frac{1}{27}$-$\frac{1}{9}$+$\frac{1}{3}$+1=$\frac{32}{27}$,
故答案为:$\frac{32}{27}$.
点评 本题主要考查利用导数研究函数的单调性,由单调性求函数的最值,余弦函数的定义域和值域,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
10.已知△ABC的三边AB=$\sqrt{{a}^{2}+{b}^{2}}$,BC=$\sqrt{{b}^{2}+{c}^{2}}$,CA=$\sqrt{{c}^{2}+{a}^{2}}$ 其中a,b,c>0,则△ABC的形状是 ( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 以上答案都不对 |
12.一个空间几何体的三视图如图所示,则这个几何体的体积为( )
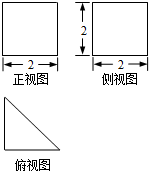

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | 8 |