题目内容
14．已知实数x，y满足$\left\{\begin{array}{l}2x+y≥0\\ 2x-y≤0\\ 0≤y≤t\end{array}\right.$其中t＞0．若z=3x+y的最大值为5，则z的最小值为（ ）| A． | $\frac{5}{2}$ | B． | 1 | C． | 0 | D． | -1 |
分析 由题意作出其平面区域，将z=3x+y化为y=-3x+z，z相当于直线y=-3x+z的纵截距，从而解方程$\left\{\begin{array}{l}{y=-3x+5}\\{y=2x}\end{array}\right.$可求出t，再代入求最小值即可．
解答 解：由题意作出其平面区域，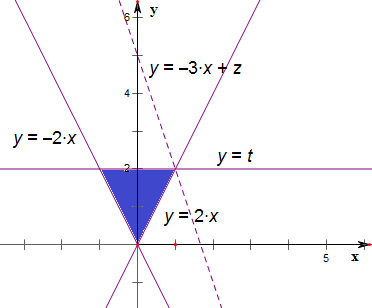
将z=3x+y化为y=-3x+z，z相当于直线y=-3x+z的纵截距，
故结合图象可得，
$\left\{\begin{array}{l}{y=-3x+5}\\{y=2x}\end{array}\right.$，
解得，x=1，y=2；
故t=2；
由$\left\{\begin{array}{l}{y=2}\\{y=-2x}\end{array}\right.$解得，
x=-1，y=2；
故z的最小值为
z=-1×3+2=-1；
故选D．
点评 本题考查了简单线性规划，作图要细致认真，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
4．
执行如图所示的程序框图，输出的s的值为（ ）
执行如图所示的程序框图，输出的s的值为（ ）| A． | $\frac{9}{5}$ | B． | $\frac{7}{4}$ | C． | $\frac{11}{6}$ | D． | $\frac{4}{5}$ |
5．已知点F1，F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右两焦点，若双曲线左支上存在点P与点F2关于直线y=$\frac{b}{a}$x对称，则双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | 2 | D． | $\sqrt{5}$ |
2．在平面直角坐标系中，O 为坐标原点，已知两点 A（1，0），B（1，1），且∠BOP=90°．设$\overrightarrow{OP}$=$\overrightarrow{OA}$+k$\overrightarrow{OB}$（k∈R），则|$\overrightarrow{OP}$|=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\sqrt{2}$ | D． | 2 |
19．在复平面内，复数z=$\frac{2-i}{（1+i）^{2}}$对应的点位于下列哪个象限（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
6．某市为了了解市民对本市文明建设的满意程度，通过问卷调查了学生、在职人员、退休人员共250人，结果如表：
若在职人员中随机抽取1人，恰好抽到学生的概率为0.32．
（1）求x的值；
（2）若y≥70，z≥2，求市民对市政管理满意度不小于0.9的概率．
（注：满意度=$\frac{满意人数}{总人数}$）
| 学生 | 在职人员 | 退休人员 | |
| 满意 | x | y | 78 |
| 不满意 | 5 | z | 12 |
（1）求x的值；
（2）若y≥70，z≥2，求市民对市政管理满意度不小于0.9的概率．
（注：满意度=$\frac{满意人数}{总人数}$）
在三棱锥D-ABC中，∠DAC=∠BAC=60°，AC=1，BA=2，AD=3，AC⊥BC，