题目内容
10.已知正数a,b,c满足a+b+c=6,求证:$\frac{1}{a(1+b)}+\frac{1}{b(1+c)}+\frac{1}{c(1+a)}≥\frac{1}{2}$.分析 由已知及均值不等式,即可证明结论.
解答 证明:由已知及均值不等式:$\frac{1}{a(1+b)}+\frac{1}{b(1+c)}+\frac{1}{c(1+a)}≥\frac{3}{{\root{3}{abc(1+a)(1+b)(1+c)}}}$
=$\frac{3}{{\root{3}{abc}•\root{3}{(1+a)(1+b)(1+c)}}}≥\frac{3}{{\frac{a+b+c}{3}•\frac{1+a+1+b+1+c}{3}}}$=$\frac{3}{2•3}=\frac{1}{2}$…(10分)
点评 本题考查不等式的证明,正确运用均值不等式是关键.

练习册系列答案
相关题目
1.已知四棱锥P-ABCD的底面四边形ABCD的对边互不平行,现用一平面α去截此四棱锥,且要使截面是平行四边形,则这样的平面α( )
| A. | 有且只有一个 | B. | 有四个 | C. | 有无数个 | D. | 不存在 |
18.过抛物线x2=4y的焦点F作倾斜角为α的直线交抛物线于P、Q两点,过点P作抛物线的切线l交y轴于点T,过点P作切线l的垂线交y轴于点N,则△PNF为( )
| A. | 等腰直角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
15.定义在R上的奇函数f(x)满足f(2-x)=f(x),且在[0,1)上单调递减,若方程f(x)=-1在[0,1)上有实数根,则方程f(x)=1在区间[-1,7]上所有实根之和是( )
| A. | 12 | B. | 14 | C. | 6 | D. | 7 |
19.执行如图所示的程序框图,则输出的S=( )
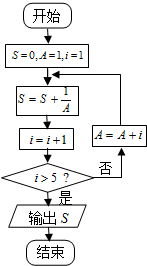

| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{8}{5}$ | D. | $\frac{12}{7}$ |
20.过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{b}$=1(a>b>0)的左顶点A且斜率为k的直线交椭圆于另一个点B,且点B在x轴上的射影恰好为右焦点F,若0<k<$\frac{1}{3}$,则椭圆的离心率的取值范围是( )
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,1) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
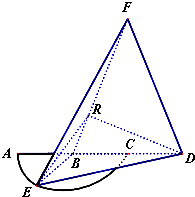 如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.
如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.