Question

【题目】已知数列是公差为正数的等差数列，其前项和为，

且，

(1)求数列的通项公式．

(2)设数列满足，

①求数列的通项公式；

②是否存在正整数，使得，，成等差数列？若存在，求出的值；若不存在，请说明理由．

Answer 1

【答案】⑴；(2)①；②见解析

【解析】

（1）直接由，列关于首项和公差的方程组，求解方程组得首项和公差，代入等差数列的通项公式得结论；（2）①把数列的通项公式代入 ,然后裂项，累加后即可求得数列的通项公式；②假设存在正整数,使得成等差数列，则，由此列关于的方程，求解得结论.

⑴由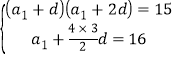得

所以

(2)①因为

则，...

各式相加得，所以

又符合上式，

所以；

②存在正整数，使得，，成等差数列，

则，即

化解整理可得，

因为

所以，所以，得，

所以或

当时，，不合题意，舍去

故存在，