题目内容
设P表示一个点,a,b表示两条直线,α,β表示两个平面,给出下列命题,其中正确的命题是( )
①P∈a,P∈α⇒a?α;
②a∩b=P,b?β⇒a?β;
③a∥b,a?α,P∈b,P∈α⇒b?α;
④α∩β=b,P∈α,P∈β⇒P∈b.
①P∈a,P∈α⇒a?α;
②a∩b=P,b?β⇒a?β;
③a∥b,a?α,P∈b,P∈α⇒b?α;
④α∩β=b,P∈α,P∈β⇒P∈b.
| A．①② | B．②③ | C．①④ | D．③④ |
D
当a∩α=P时, P∈a,P∈α,但a?α,∴①错;当a∩β=P时,
②错;如图,∵a∥b,P∈b,∴P∉a,
∴由直线a与点P确定唯一平面α,
又a∥b,由a与b确定唯一平面β,但β过直线a与点P,∴β与α重合,∴b?α,故③正确;两个平面的公共点必在其交线上,故④正确.
【误区警示】解答本题时对平面性质不熟、不善于举出反例是致错的主要原因.
②错;如图,∵a∥b,P∈b,∴P∉a,
∴由直线a与点P确定唯一平面α,
又a∥b,由a与b确定唯一平面β,但β过直线a与点P,∴β与α重合,∴b?α,故③正确;两个平面的公共点必在其交线上,故④正确.
【误区警示】解答本题时对平面性质不熟、不善于举出反例是致错的主要原因.
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
),连接MN.
的值．
均不在平面
内，给出下列命题：
，则
；②若
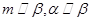，则
，则
，则