题目内容
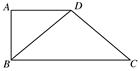
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )

| A.平面ABD⊥平面ABC | B.平面ADC⊥平面BDC |
| C.平面ABC⊥平面BDC | D.平面ADC⊥平面ABC |
D
由题意知,在四边形ABCD中,CD⊥BD.
在三棱锥A-BCD中,平面ABD⊥平面BCD,两平面的交线为BD,
所以CD⊥平面ABD,因此有AB⊥CD.
又因为AB⊥AD,AD∩DC=D,所以AB⊥平面ADC,于是得到平面ADC⊥平面ABC.
在三棱锥A-BCD中,平面ABD⊥平面BCD,两平面的交线为BD,
所以CD⊥平面ABD,因此有AB⊥CD.
又因为AB⊥AD,AD∩DC=D,所以AB⊥平面ADC,于是得到平面ADC⊥平面ABC.

练习册系列答案
相关题目
 AD,BE∥=
AD,BE∥=
 AB.直角梯形ACEF中,
AB.直角梯形ACEF中, ,
, 是锐角,且平面ACEF⊥平面ABCD.
是锐角,且平面ACEF⊥平面ABCD.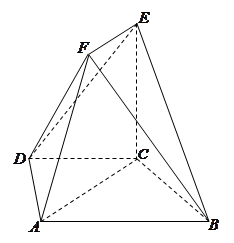
 ;
; ,试求
,试求 中,点
中,点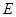 为边
为边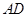 上的点,点
上的点,点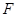 为边
为边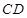 的中点,
的中点,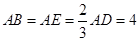 ,现将
,现将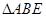 沿
沿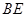 边折至
边折至 位置,且平面
位置,且平面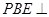 平面
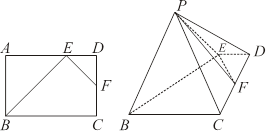
平面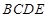 .
.
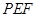 ;
;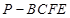 的体积.
的体积. ∥
∥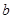 ,
, 平面
平面 ,则
,则 定义域内存在
定义域内存在 满足
满足
 ,则
,则