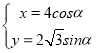题目内容
【题目】已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,依此类推,若该数列前
,依此类推,若该数列前![]() 项和
项和![]() 满足:①
满足:①![]() ②
②![]() 是2的整数次幂,则满足条件的最小的
是2的整数次幂,则满足条件的最小的![]() 为
为
A. 21B. 91C. 95D. 10
【答案】C
【解析】
构造数列![]()
![]() ,使得:
,使得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求出数列
,求出数列![]() 的前
的前![]() 项和,根据题意可表示出原数列
项和,根据题意可表示出原数列![]() 与
与![]() 的关系,以及原数列前
的关系,以及原数列前![]() 和与数列
和与数列![]() 的前
的前![]() 项和的关系,讨论出满足条件的
项和的关系,讨论出满足条件的![]() 的最小值即可。
的最小值即可。
根据题意构造数列![]()
![]() ,使得:
,使得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,所以数列
,所以数列![]() 的前
的前![]() 项和
项和![]() 令数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,为
令数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,为![]() ,
,
根据题意可得:![]() ,
,![]() ,则数列
,则数列![]() 的前
的前![]() 项和
项和![]()
![]() ,
,
所以要使数列![]() 前
前![]() 项和
项和![]() 满足:
满足:![]() ,则
,则![]() ,则
,则![]() ,故
,故![]() ,故D答案不对。
,故D答案不对。
由于![]() 是2的整数次幂,则
是2的整数次幂,则![]() ,则
,则![]() ,则
,则![]() ,
,
当![]() 时,则
时,则![]() ,解得:
,解得:![]() ,
,![]() ,
,
故满足条件的最小的![]() 为95,
为95,
故答案选C

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目