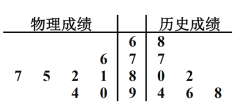
ћвƒњƒЏ»Ё
°Њћвƒњ°њ∆фґЂ –’юЄЃƒв‘ЏµыЇюљ®“їЄц¬√”ќєџєвѕоƒњ,…иЉ∆Јљ∞Є»зѕ¬£Ї»зЌЉЋщ Њµƒ‘≤O «‘≤–ќЇюµƒ±яљз,—ЎѕяґќAB,BC,CD,DAљ®“їЄцєџЊ∞≥§ј»,∆д÷–A,B,C,D «єџЊ∞≥§ј»µƒЋƒЄц≥ц»лњЏ«“ґЉ‘Џ‘≤O…ѕ£ђ“—÷™£ЇBC=12∞ў√„,AB=8∞ў√„,‘ЏЇю÷–Pі¶ЇЌЇю±яDі¶Єчљ®“їЄцєџЊ∞Ќ§,«“Ћь√«єЎ”Џ÷±ѕяACґ‘≥∆,‘ЏЇю√жљ®“їћхєџЊ∞«≈APC.єџЊ∞Ќ§µƒіу–°°ҐєџЊ∞≥§ј»°ҐєџЊ∞«≈µƒњнґ»ЊщЇц¬‘≤їЉ∆£ђ…и![]() £Ѓ
£Ѓ
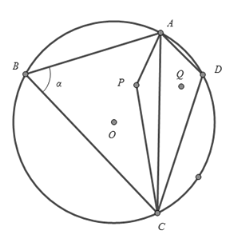
£®1£©»фєџЊ∞≥§ј»AD£љ4∞ў√„£ђCD=AB£ђ«у”…єџЊ∞≥§ј»ЋщќІ≥…µƒЋƒ±я–ќABCDƒЏµƒЇю√ж√жїэ£ї
£®2£©µ±![]() ±£ђ«у»эљ«–ќ«ш”тADCƒЏµƒЇю√ж√жїэµƒ„оіу÷µ£ї
±£ђ«у»эљ«–ќ«ш”тADCƒЏµƒЇю√ж√жїэµƒ„оіу÷µ£ї
£®3£©»фCD=8∞ў√„«“єжїЃљ®Ќ§µгP‘Џ»эљ«–ќABC«ш”тƒЏ£®≤ї∞ьј®±яљз£©£ђ ‘≈–ґѕЋƒ±я–ќABCPƒЏЇю√ж√жїэ «Јс”–„оіу÷µ£њ»ф”–£ђ«у≥ц„оіу÷µ£ђ≤Ґ–і≥ціЋ ±![]() µƒ÷µ£ї»ф√ї”–£ђ«лЋµ√чјн”…£Ѓ
µƒ÷µ£ї»ф√ї”–£ђ«лЋµ√чјн”…£Ѓ
°Њір∞Є°њ£®1£©![]() ∆љЈљ∞ў√„£ї£®2£©
∆љЈљ∞ў√„£ї£®2£©![]() ∆љЈљ∞ў√„£ї£®3£©µ±
∆љЈљ∞ў√„£ї£®3£©µ±![]() =
=![]() ±£ђЋƒ±я–ќABCPƒЏµƒЇю√ж√жїэ»°µљ„оіу÷µ£ђ „оіу÷µќ™32∆љЈљ∞ў√„.
±£ђЋƒ±я–ќABCPƒЏµƒЇю√ж√жїэ»°µљ„оіу÷µ£ђ „оіу÷µќ™32∆љЈљ∞ў√„.
°Њљвќц°њ
£®1£©Ј÷±р‘Џ![]() ЇЌ
ЇЌ![]() ÷–‘Ћ”√”аѕ“ґ®јн£ђ«у≥ц
÷–‘Ћ”√”аѕ“ґ®јн£ђ«у≥ц![]() £ђљшґшњ…µ√
£ђљшґшњ…µ√![]() ЇЌ
ЇЌ![]() £ђЄщЊЁ
£ђЄщЊЁ![]() Љіњ…µ√љбєы£ї£®2£©‘Џ
Љіњ…µ√љбєы£ї£®2£©‘Џ![]() ÷–£ђњ…µ√
÷–£ђњ…µ√![]() £ђЅо
£ђЅо![]() £ђ
£ђ![]() £ђ‘Џ
£ђ‘Џ![]() ÷–£ђ‘Ћ”√”аѕ“ґ®јнњ…µ√
÷–£ђ‘Ћ”√”аѕ“ґ®јнњ…µ√![]() £ђ”…їщ±Њ≤їµ» љњ…µ√
£ђ”…їщ±Њ≤їµ» љњ…µ√![]() £ђ”…
£ђ”…![]() Љіњ…µ√љбєы£ї£®3£©ѕ»«у≥ц
Љіњ…µ√љбєы£ї£®3£©ѕ»«у≥ц![]() £ђЉ∆Ћг≥ц
£ђЉ∆Ћг≥ц![]() £ђљшґшњ…µ√љбєы.
£ђљшґшњ…µ√љбєы.
љв£Ї£®1£©°яЋƒ±я–ќABCDƒЏљ””Џ‘≤O£ђ°а![]() ABC+
ABC+![]() ADC=
ADC=![]()
‘Џ![]() ÷–£ђ
÷–£ђ![]()
‘Џ![]() ÷–£ђ
÷–£ђ![]()
љвµ√![]() £ђ°а
£ђ°а![]()
°а![]()
£®∆љЈљ∞ў√„£©
ір£ЇЋƒ±я–ќABCDƒЏµƒЇю√ж√жїэ «![]() ∆љЈљ∞ў√„.
∆љЈљ∞ў√„.
£®2£©°я![]() =60
=60![]() £ђ°а‘Џ
£ђ°а‘Џ![]() ÷–£ђ
÷–£ђ![]() =112
=112
Ѕо![]() £ђ
£ђ![]() £ђ ‘Џ
£ђ ‘Џ![]() ÷–£ђ
÷–£ђ![]() =112
=112
°а![]() =112
=112
°я![]()
°а![]() £®µ±«“љцµ±x=y ±£ђ»°µ»Ї≈£©
£®µ±«“љцµ±x=y ±£ђ»°µ»Ї≈£©
°я![]()
°а![]() £®∆љЈљ∞ў√„£©
£®∆љЈљ∞ў√„£©
ір£Ї»эљ«–ќ«ш”тADCƒЏµƒЇю√ж√жїэ„оіу÷µ![]() ∆љЈљ∞ў√„£Ѓ
∆љЈљ∞ў√„£Ѓ
£®3£©°яµгPЇЌµгDєЎ”Џ÷±ѕяACґ‘≥∆£ђ
°а![]() APC=
APC=![]() ADC£ђPC=CD=8
ADC£ђPC=CD=8
”…£®1£©÷™![]() ABC+
ABC+![]() ADC=
ADC=![]() £ђ°а
£ђ°а![]() ABC+
ABC+![]() APC=
APC=![]()
°я![]() ABC=
ABC=![]() £ђ°а
£ђ°а![]() APC=
APC=![]()
![]()
°яµгP‘Џ![]() «ш”тƒЏ
«ш”тƒЏ
°а![]() £ђ°а
£ђ°а![]()
°я‘Џ![]() ÷–£ђ
÷–£ђ![]()
‘Џ![]() ÷–£ђ
÷–£ђ![]()
°а![]()
љвµ√![]() їт
їт![]() £®…б»•£©
£®…б»•£©
![]()
![]()
°я![]() £ђ°аЋƒ±я–ќABCPƒЏµƒЇю√ж√жїэ”–„оіу÷µ£ђ
£ђ°аЋƒ±я–ќABCPƒЏµƒЇю√ж√жїэ”–„оіу÷µ£ђ
ір£Їµ±![]() =
=![]() ±£ђЋƒ±я–ќABCPƒЏµƒЇю√ж√жїэ»°µљ„оіу÷µ£ђ„оіу÷µќ™32∆љЈљ∞ў√„
±£ђЋƒ±я–ќABCPƒЏµƒЇю√ж√жїэ»°µљ„оіу÷µ£ђ„оіу÷µќ™32∆љЈљ∞ў√„

 ‘ƒґЅњм≥µѕµЅ–ір∞Є
‘ƒґЅњм≥µѕµЅ–ір∞Є