题目内容
为了让学生了解更多“社会法律”知识,某中学举行了一次“社会法律知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
| 分组 | 频数 | 频率 |
| 60.5~70.5 | ① | 0.16 |
| 70.5~80.5 | 10 | ?② |
| 80.5~90.5 | 18 | 0.36 |
| 90.5~100.5 | ③ | ④ |
| 合计 | 50 | 1 |
(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为
000,001,002,…,799,试写出第二组第一位学生的编号 ;
(2)填充频率分布表的空格① ② ③ ④ 并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
(1)016 ;(2) 1 8 2 0.28 3 14 4 0.20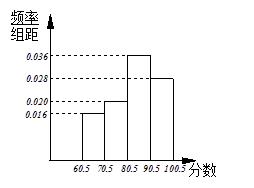 ;(3)256.
;(3)256.
解析试题分析:(1)编号为016- -2分
(2) 1 8 2 0.28 3 14 4 0.20- 每空1分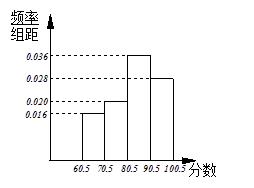
2分
在被抽到的学生中获二奖的人数是9+7=16人, 1分
占样本的比例是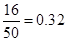 , 1分
, 1分
所以获二等奖的人数估计为800×32%=256人. 1分
答:获二等奖的大约有256人. 1分
考点:系统抽样;频率分布表;频率分布直方图。
点评:此题主要考查频率分布直方图。在频率分布直方图中,小长方形的面积就是这组数据的频率。此题属于基础题型。

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
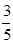 .
.(1)请将上面的列联表补充完整;
(2)是否在犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关?说明你的理由.下面的临界值表供参考:
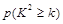 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005] | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
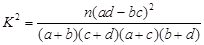 ,其中
,其中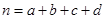 )
)
某中学共2200名学生中有男生1200名,按男女性别用分层抽样抽出110名学生,询问是否爱好某项运动。已知男生中有40名爱好该项运动,女生中有30名不爱好该项运动。
(1)如下的列联表:
| | 男 | 女 | 总计 |
| 爱好 | 40 | | |
| 不爱好 | | 30 | |
| 总计 | | | |
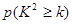 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
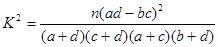
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
性别与看营养说明列联表 单位: 名
| | 男 | 女 | 总计 |
| 看营养说明 | 50 | 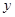 | 80 |
| 不看营养说明 |  | 20 | 30 |
| 总计 | 60 | 50 | 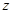 |
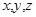 的值.
的值.(2)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
(理科)(本小题满分12分)PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095 – 2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米 ~ 75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标。从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
| PM2.5日均值 (微克/立方米) | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
| 频数 | 3 | 1 | 1 | 1 | 1 | 3 |
在某次测验中,有6位同学的平均成绩为75分.用 表示编号为
表示编号为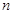
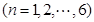 的同学所得成绩,且前5位同学的成绩如下:
的同学所得成绩,且前5位同学的成绩如下:
编号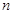 | 1 | 2 | 3 | 4 | 5 |
成绩 | 70 | 76 | 72 | 70 | 72 |
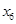 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差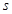 ;
;(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.

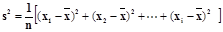 )
)
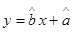 ;
;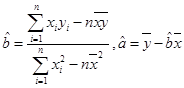 ).
).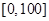 ,样本数据分组为
,样本数据分组为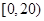 ,
,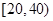 ,
,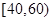 ,
,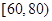 ,
,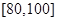 .
.
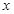 的值;
的值;