题目内容
以下茎叶图记录了甲、乙两组各四名同学的植树棵树。乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(1)求甲组同学植树棵树的平均数和方差;(参考公式: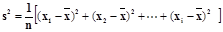 )
)
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
(1)10,1;(2)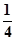 .
.
解析试题分析:(1)甲的平均数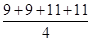 =10,
=10,
方差为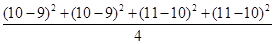 =1;
=1;
(2)甲乙两组植树情况共有4×4=16种结果。其中两名同学的植树总棵数为19的情况有:(9,10),(9,10)(11,8),(11,8),所以由古典概型概率的计算公式得这两名同学的植树总棵数为19的概率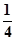 。
。
考点:本题主要考查茎叶图,平均数、方差的计算,古典概型概率的计算。
点评:中档题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。古典概型概率的计算问题,关键是明确基本事件数,往往借助于“树图法”,做到不重不漏。本题较为容易。

对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如下表:
| 寿命(h) | 频率 |
| 500600 | 0.10 |
| 600700 | 0.15 |
| 700800 | 0.40 |
| 800900 | 0.20 |
| 9001000 | 0.15 |
| 合计 | 1 |
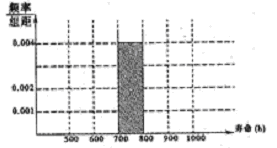
(I)在下图中补齐频率分布直方图;
(II)估计元件寿命在500800h以内的概率。
近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 男 | | 5 | |
| 女 | 10 | | |
| 合计 | | | 50 |
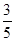 .
.(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有
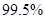 的把握认为患心肺疾病与性别有关?说明你的理由;
的把握认为患心肺疾病与性别有关?说明你的理由;(Ⅲ)已知在患心肺疾病的10位女性中,有3位又患胃病.现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为
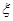 ,求
,求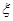 的分布列,数学期望以及方差.
的分布列,数学期望以及方差.下面的临界值表供参考:
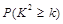 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
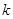 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
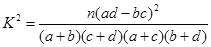 其中
其中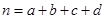 )
) 为了让学生了解更多“社会法律”知识,某中学举行了一次“社会法律知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
| 分组 | 频数 | 频率 |
| 60.5~70.5 | ① | 0.16 |
| 70.5~80.5 | 10 | ?② |
| 80.5~90.5 | 18 | 0.36 |
| 90.5~100.5 | ③ | ④ |
| 合计 | 50 | 1 |
(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为
000,001,002,…,799,试写出第二组第一位学生的编号 ;
(2)填充频率分布表的空格① ② ③ ④ 并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
第 届亚运会于
届亚运会于 年
年 月
月 日至
日至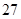 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了 名男志愿者和
名男志愿者和 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有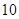 人和
人和 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下 列联表:
列联表:
| | 喜爱运动 | 不喜爱运动 | 总计 |
| 男 | 10 | | 16 |
| 女 | 6 | | 14 |
| 总计 | | | 30 |
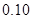 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?(3)如果从喜欢运动的女志愿者中(其中恰有
 人会外语),抽取
人会外语),抽取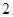 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中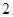 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?附:K2=
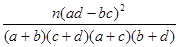
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5(PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称可入肺颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,15] | 4 | 0.1 |
| 第二组 | (15,30] | 12 | 0.3 |
| 第三组 | (30,45] | 8 | 0.2 |
| 第四组 | (45,60] | 8 | 0.2 |
| 第三组 | (60,75] | 4 | 0.1 |
| 第四组 | (75,90) | 4 | 0.1 |
(Ⅱ)求该样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由;
(Ⅲ)将频率视为概率,对于去年的某2天,记这2天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为
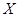 ,求
,求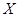 的分布列及数学期望
的分布列及数学期望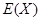 .
. 由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图示:
| | |
| 4 | 3 5 6 6 6 7 7 7 8 8 9 9 |
| 5 | 0 1 1 2 |
| | |
指出这组数据的众数和中位数;
若视力测试结果不低于5.0,则称为“健康视力”,求校医从这16人中随机选取3人,至多有1人是“健康视力”的概率;以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记
 表示抽到“健康视力”学生的人数,求
表示抽到“健康视力”学生的人数,求 的分布列及数学期望
的分布列及数学期望 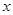 与销售额
与销售额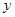 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据: