题目内容
12.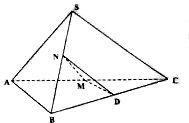 已知三棱锥S-ABC中△SAB与△ABC均为等边三角形,M、N分别为AC、SB的中点,经过M、N且与AB平行的平面α与BC交于点D.
已知三棱锥S-ABC中△SAB与△ABC均为等边三角形,M、N分别为AC、SB的中点,经过M、N且与AB平行的平面α与BC交于点D.(1)求证:SC∥面MND;
(2)证明:SC⊥MD.
分析 (1)由条件利用直线和平面平行的性质可得AB∥MD,D为BC的中点,可得SC∥ND,再利用直线和平面平行的判定定理证得SC∥面MND.
(2)取AB的中点为O,根据AB⊥SO,AB⊥CO,证明AB⊥平面SOC,可得AB⊥SC,从而证得MD⊥SC.
解答 (1)证明:∵M、N分别为AC、SB的中点,经过M、N且与AB平行的平面α与BC交于点D,
故AB∥MD,∴D为BC的中点,故NC为△SBC的中位线,∴SC∥ND.
而ND?面MND,∴SC∥面MND.
(2)证明:取AB的中点为O,则由△SAB与△ABC均为等边三角形,可得AB⊥SO,AB⊥CO.
而SO∩CO=O,∴AB⊥平面SOC,∴AB⊥SC,∴MD⊥SC.
点评 本题主要考查直线和平面平行的性质定理和判定定理,直线和平面垂直判定定理的应用,属于基础题.

练习册系列答案
相关题目

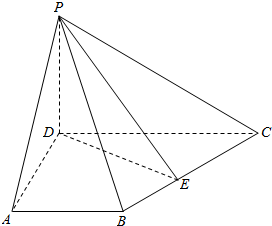 如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点.
如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点.