题目内容
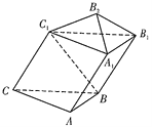
【题目】已知在四棱柱ABCD—A1B1C1D1中,底面ABCD是菱形,且平面A1ADD1⊥平面ABCD,DA1=DD1,点E,F分别为线段A1D1,BC的中点.
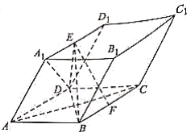
(1)求证:EF∥平面CC1D1D;
(2)求证:AC⊥平面EBD.
【答案】(1)证明见解析;(2)证明见解析;
【解析】
(1)连接![]() ,通过证明四边形
,通过证明四边形![]() 是平行四边形,证得
是平行四边形,证得![]() ,由此证得
,由此证得![]() 平面
平面![]() .
.
(2)通过证明![]() ,结合面面垂直的性质定理证得
,结合面面垂直的性质定理证得![]() 平面
平面![]() ,由此证得
,由此证得![]() ,由菱形的性质得到
,由菱形的性质得到![]() ,从而证得
,从而证得![]() 平面
平面![]() .
.
(1)连结CD1,四棱柱ABCD—A1B1C1D1中,A1B1C1D1,BB1C1C是平行四边形,
∴A1D1//B1C1,BC//B1C1,且A1D1=B1C1,BC=B1C1,
又∵点E,F分别为线段AD,BC的中点,
∴ED1//FC,ED1=FC,
所以四边形ED1CF是平行四边形,
∴EF//CD1,又∵EF![]() 平面CC1D1D,CD
平面CC1D1D,CD![]() 平面CC1D1D,
平面CC1D1D,
∴EF//平面CC1D1D.
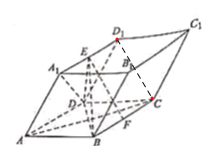
(2)四棱柱ABCD—A1B1C1D1中,四边形AA1D1D是平行四边形,
∴AD//A1D1,在△DA1D1中,DA1=DD1,点E为线段A1D1的中点,
∴DE⊥A1D1,又∵AD//A1D1,∴DE⊥AD,
又∵平面A1ADD1⊥平面ABCD,平面A1ADD1![]() 平面ABCD=AD,DE
平面ABCD=AD,DE![]() 平面A1ADD1,
平面A1ADD1,
∴DE⊥平面ABCD,又AC![]() 平面ABCD,∴DE⊥AC,
平面ABCD,∴DE⊥AC,
∵底面ABCD是菱形,∴BD⊥AC,
又∵BD![]() DE=D,BD,DE
DE=D,BD,DE![]() 平面EBD,
平面EBD,
∴AC⊥平面EBD.

 阅读快车系列答案
阅读快车系列答案【题目】福利彩票“双色球”中红色球由编号为![]() 的
的![]() 个球组成.某彩民利用下面的随机数表选取
个球组成.某彩民利用下面的随机数表选取![]() 组数作为
组数作为![]() 个红色球的编号,选取方法是从随机数表(如下)第
个红色球的编号,选取方法是从随机数表(如下)第![]() 行的第
行的第![]() 列数字开始从左向右依次选取两个数字,则选出来的第
列数字开始从左向右依次选取两个数字,则选出来的第![]() 个红色球的编号为( )
个红色球的编号为( )
49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 17 34 91 64 |
57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】![]() 年下半年以来,各地区陆续出台了“垃圾分类”的相关管理条例,实行“垃圾分类”能最大限度地减少垃圾处置量,实现垃圾资源利用,改善垃圾资源环境,某部门在某小区年龄处于
年下半年以来,各地区陆续出台了“垃圾分类”的相关管理条例,实行“垃圾分类”能最大限度地减少垃圾处置量,实现垃圾资源利用,改善垃圾资源环境,某部门在某小区年龄处于![]() 岁的人中随机地抽取
岁的人中随机地抽取![]() 人,进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到如图示各年龄段人数的频率分布直方图和表中的统计数据.
人,进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到如图示各年龄段人数的频率分布直方图和表中的统计数据.
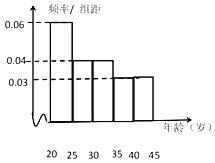
组数 | 分组 | “环保族”人数 | 占本组的频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)根据频率分布直方图,估计这![]() 人年龄的平均值(同一组数据用该区间的中点值代替,结果按四舍五入保留整数);
人年龄的平均值(同一组数据用该区间的中点值代替,结果按四舍五入保留整数);
(3)从年龄段在![]() 的“环保族”中采取分层抽样的方法抽取
的“环保族”中采取分层抽样的方法抽取![]() 人进行专访,并在这
人进行专访,并在这![]() 人中选取
人中选取![]() 人作为记录员,求选取的
人作为记录员,求选取的![]() 名记录员中至少有一人年龄在
名记录员中至少有一人年龄在![]() 中的概率.
中的概率.