题目内容
【题目】如图,在四棱锥![]() 中,四边形ABCD是平行四边形,
中,四边形ABCD是平行四边形,![]() ,
,![]() ,
,![]() .
.
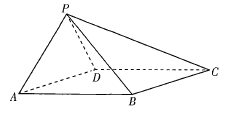
(1)求PC的长;
(2)求AP与平面PBC所成角的正弦值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)取AD的中点E,连接PE,BE,由等边三角形的性质可得![]() ,由勾股定理可得
,由勾股定理可得![]() ,则
,则![]() 平面PBE,即
平面PBE,即![]() ,由平行四边形可得
,由平行四边形可得![]() ,进而求解;
,进而求解;
(2)过点A作平面PBC的垂线,垂足为H,连接PH,则![]() 即AP与平面PBC所成的角,由(1)可得
即AP与平面PBC所成的角,由(1)可得![]() 平面PBE,则
平面PBE,则![]() 平面PBE,即可证得
平面PBE,即可证得![]() 平面PBC,由
平面PBC,由![]() 平面PBC可得
平面PBC可得![]() ,进而利用勾股定理求得
,进而利用勾股定理求得![]() ,即可求解.
,即可求解.
解:(1)如图,取AD的中点E,连接PE,BE,因为![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,
,![]() 平面PBE,所以
平面PBE,所以![]() 平面PBE,
平面PBE,
又![]() 平面PBE,所以
平面PBE,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() .
.
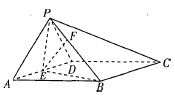
(2)过点A作平面PBC的垂线,垂足为H,连接PH,则![]() 即AP与平面PBC所成的角,
即AP与平面PBC所成的角,
过E作PB的垂线交PB于点F,因为![]() ,
,![]() 平面PBE,
平面PBE,
所以![]() 平面PBE,所以
平面PBE,所以![]() ,
,
又![]() ,
,![]() ,PB,
,PB,![]() 平面PBC,
平面PBC,
所以![]() 平面PBC,
平面PBC,
因为![]() ,所以
,所以![]() 平面PBC,所以
平面PBC,所以![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
因此![]() ,
,
所以 .
.


【题目】海南盛产各种名贵树木,如紫檀、黄花梨等.在实际测量单根原木材体积时,可以检量木材的实际长度(检尺长)和小头直径(检尺径),再通过国家公布的原木材积表直接查询得到,原木材积表的部分数据如下所示:
检尺径 ( | 检尺长( | ||||
2.0 | 2.2 | 2.4 | 2.5 | 2.6 | |
材积( | |||||
8 | 0.0130 | 0.0150 | 0.0160 | 0.0170 | 0.0180 |
10 | 0.0190 | 0.0220 | 0.0240 | 0.0250 | 0.0260 |
12 | 0.0270 | 0.0300 | 0.0330 | 0.0350 | 0.0370 |
14 | 0.0360 | 0.0400 | 0.0450 | 0.0470 | 0.0490 |
16 | 0.0470 | 0.0520 | 0.0580 | 0.0600 | 0.0630 |
18 | 0.0590 | 0.0650 | 0.0720 | 0.0760 | 0.0790 |
20 | 0.0720 | 0.0800 | 0.0880 | 0.0920 | 0.0970 |
22 | 0.0860 | 0.0960 | 0.1060 | 0.1110 | 0.1160 |
24 | 0.1020 | 0.1140 | 0.1250 | 0.1310 | 0.1370 |
若小李购买了两根紫檀原木,一根检尺长为![]() ,检尺径为
,检尺径为![]() ,另一根检尺长为
,另一根检尺长为![]() ,检尺径为
,检尺径为![]() ,根据上表,可知两根原木的材积之和为______
,根据上表,可知两根原木的材积之和为______![]() .
.