Question

6．已知点O（0，0），A（1，2），B（4，5），$\overrightarrow{OP}$=t₁$\overrightarrow{OA}$+t₂$\overrightarrow{AB}$．
（1）证明：当t₁=1时，不论t₂为何实数，A、B、P三点共线；
（2）试求当t₁、t₂满足什么条件时，O、A、B、P能组成一个平行四边形．

Answer 1

分析 （1）把t₁=1代入$\overrightarrow{OP}$=t₁$\overrightarrow{OA}$+t₂$\overrightarrow{AB}$化简，利用向量共线的条件即可证明结论；
（2）设P的坐标是（x，y），根据向量的坐标运算和向量相等的条件化简$\overrightarrow{OP}$=t₁$\overrightarrow{OA}$+t₂$\overrightarrow{AB}$，求出p点的坐标，由平行四边形的性质可得$\overrightarrow{OA}=\overrightarrow{PB}$，利用向量相等、坐标运算列出方程组求解．

解答 证明：（1）由题意知，t₁=1，代入$\overrightarrow{OP}$=t₁$\overrightarrow{OA}$+t₂$\overrightarrow{AB}$得，
$\overrightarrow{OP}$=$\overrightarrow{OA}$+t₂$\overrightarrow{AB}$，则$\overrightarrow{OP}$-$\overrightarrow{OA}$=t₂$\overrightarrow{AB}$，即$\overrightarrow{AP}$=t₂$\overrightarrow{AB}$，
所以当t₁=1时，不论t₂为何实数，A、B、P三点共线；
（2）设P的坐标是（x，y），
由O（0，0），A（1，2），B（4，5）得，$\overrightarrow{OA}$=（1，2），$\overrightarrow{AB}$=（3，3），
因为$\overrightarrow{OP}$=t₁$\overrightarrow{OA}$+t₂$\overrightarrow{AB}$，所以（x，y）=t₁（1，2）+t₂（3，3），
解得x=t₁+3t₂，y=2t₁+3t₂，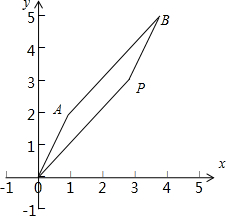
若四边形OABP能成为平行四边形，
如图所得，$\overrightarrow{OA}=\overrightarrow{PB}$，
即（1，2）=（4-t₁-3t₂，5-2t₁-3t₂），
所以$\left\{\begin{array}{l}{1=4-{t}_{1}-3{t}_{2}}\\{2=5-2{t}_{1}-3{t}_{2}}\end{array}\right.$，得$\left\{\begin{array}{l}{{t}_{1}+3{t}_{2}=3}\\{2{t}_{1}+3{t}_{2}=3}\end{array}\right.$，解得$\left\{\begin{array}{l}{{t}_{1}=0}\\{{t}_{2}=1}\end{array}\right.$，
所以当t₁=0、t₂=1时，O、A、B、P能组成一个平行四边形．

点评 本题考查向量的坐标运算和向量相等的条件，以向量共线的条件，属于中档题．