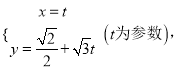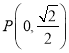题目内容
【题目】已知函数![]() ,若
,若![]() 存在唯一的零点
存在唯一的零点![]() ,且
,且![]() ,则实数
,则实数![]() _______
_______
【答案】![]()
【解析】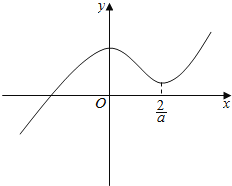
(i)当a=0时,f(x)=3x2+1,令f(x)=0,解得x=±![]() ,函数f(x)有两个零点,舍去。
,函数f(x)有两个零点,舍去。
(ii)当a≠0时,f′(x)=3ax26x=3ax(x![]() ),令f′(x)=0,解得x=0或2a.
),令f′(x)=0,解得x=0或2a.
①当a<0时, ![]() <0,当x<
<0,当x<![]() 或x>0时,f′(x)<0,此时函数f(x)单调递减;当
或x>0时,f′(x)<0,此时函数f(x)单调递减;当![]() <x<0时,f′(x)>0,此时函数f(x)单调递增。
<x<0时,f′(x)>0,此时函数f(x)单调递增。
∴![]() 是函数f(x)的极小值点,0是函数f(x)的极大值点。
是函数f(x)的极小值点,0是函数f(x)的极大值点。
∵函数f(x)=ax33x2+1存在唯一的零点x0,且x0<0,则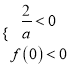 ,无解,舍去。
,无解,舍去。
②当a>0时, ![]() >0,当x>
>0,当x>![]() 或x<0时,f′(x)>0,此时函数f(x)单调递增;当0<x<
或x<0时,f′(x)>0,此时函数f(x)单调递增;当0<x<![]() 时,f′(x)<0,此时函数f(x)单调递减。
时,f′(x)<0,此时函数f(x)单调递减。
∴![]() 是函数f(x)的极小值点,0是函数f(x)的极大值点。
是函数f(x)的极小值点,0是函数f(x)的极大值点。
∵函数f(x)=ax33x2+1存在唯一的零点x0,且x0<0,则f(![]() >0,即
>0,即![]()
![]() +1>0,a>0,解得a>2.
+1>0,a>0,解得a>2.
综上可得:实数a的取值范围是(2,+∞).
故答案为:(2,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)请根据上面的数据分析该地区的老年人需要志愿者提供帮助与性别有关吗