题目内容
【题目】已知△ABC中,角A,B,C所对的边分别为a,b,c,若sin2 A+sin2 B=sin2C+sin AsinB,ccosB=b(1﹣cosC). 
(1)判断△ABC的形状;
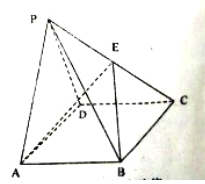
(2)在△ABC的边AB,AC上分别取D,E两点,使沿线段DE折叠三角形时,顶点A正好落在边BC上的P点处,设∠BDP=θ,当AD最小时,求 ![]() 的值.
的值.
【答案】
(1)解:由sin2A+sin2B=sin2C+sinAsinB得a2+b2=c2+ab
∴ ![]()
又0<C<π∴ ![]()
又由 ccosB=b(1﹣cosC)得:sinCcosB=sinB(1﹣cosC)
∴sinCcosB+sinBcosC=sinB∴sin(B+C)=sinB
即sinA=sinB∴a=b
故△ABC为等边三角形
(2)解:如图:连结AP,

∵AD=DP∴θ=2∠BAP
∴ ![]()
又设AD=DP=y,AB=a,则BD=a﹣y
在△BDP中,由正弦定理有: ![]()
∴ ![]()
故 
![]()
∴ ![]() 时
时 ![]()
此时 ![]()
【解析】(1)利用正弦定理以及余弦定理,结合两角和与差的三角函数,判断三角形的形状.(2)连结AP,设AD=DP=y,AB=a,则BD=a﹣y,由正弦定理求出表达式,通过三角函数的最值求解就.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目