题目内容
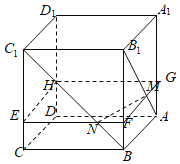
【题目】在正方体ABCD-A1B1C1D1中，点M、N分别在AB1、BC1上，且AM=
AB1，BN=BC1，则下列结论：①AA1⊥MN；②A1C1// MN；③MN//平面A1B1C1D1；④B1D1⊥MN，其中，
正确命题的个数是（ ）
A.1B.2C.3D.4
【答案】B
【解析】
由题意在四条棱A1A，B1B，C1C，D1D上分别取点G，F，E，H四点，使AG
A1A，BFB1B，CEC1C，DHD1D，得到平面GFEH，则点M，N在与平面A1B1C1D1平行的平面GFEH中．利用线面垂直的性质判断①正确；利用平行公理判断②错误；利用面面平行的性质判断③正确；利用面面平行以及线线垂直的性质判断④错误．
在正方体ABCD﹣A1B1C1D1的四条棱A1A，B1B，C1C，D1D上分别取点G，F，E，H四点，
使AGA1A，BFB1B，CEC1C，DHD1D，连接GF，FE，EH，HG，
∵点M、N分别在AB1、BC1上，且AMAB1，BNBC1，
∴M在线段GF上，N点在线段FE上．且四边形GFEH为正方形，平面GFEH∥平面A1B1C1D1，
∵AA1⊥平面A1B1C1D1，∴AA1⊥平面GFEH，
∵MN平面GFEH，∴AA1⊥MN，故①正确；
∵A1C1∥GE，而GE与MN不平行，∴A1C1与MN不平行，故②错误；
∵平面GFEH∥平面A1B1C1D1，MN平面GFEH，∴MN∥平面A1B1C1D1，故③正确；
∵B1D1∥FH，FH平面GFEH，MN平面GFEH，且MN与FH不垂直，∴B1D1与MN不垂直，故④错误．
∴正确命题只有①③．
故选：B．
【题目】某家庭为了解冬季用电量
（度）与气温
之间的关系，随机统计了某5天的用电量与当天气温，并制作了对照表，经过统计分析，发现气温在一定范围内时，用电量与气温具有线性相关关系：
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
（1）求出用电量关于气温
的线性回归方程；
（2）在这5天中随机抽取两天，求至少有一天用电量低于10（度）的概率.
（附：回归直线方程的斜率和截距的最小二乘法估计公式为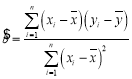
，
）
