题目内容
【题目】在平面直角坐标系中，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l上两点M，N的极坐标分别为（2，0），（
），圆C的参数方程
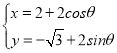（θ为参数）．
（Ⅰ）设P为线段MN的中点，求直线OP的平面直角坐标方程；
（Ⅱ）判断直线l与圆C的位置关系．
【答案】见解析
【解析】
（Ⅰ）设P为线段MN的中点，求直线OP的平面直角坐标方程；（Ⅱ）求出圆的圆心与半径，判断圆心与直线的距离与半径的关系，即可判断直线l与圆C的位置关系．
解：（Ⅰ）M，N的极坐标分别为（2，0），（
），
所以M、N的直角坐标分别为：M（2，0），N（0，
），P为线段MN的中点（1，
），
直线OP的平面直角坐标方程y
；
（Ⅱ）圆C的参数方程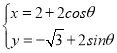
（θ为参数）．它的直角坐标方程为：（x﹣2）2+（y
）2＝4，
圆的圆心坐标为（2，
），半径为2，
直线l上两点M，N的极坐标分别为（2，0），（），
方程为y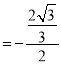
（x﹣2）
（x﹣2），即
x+3y﹣2
0．
圆心到直线的距离为：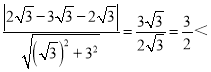
2，
所以，直线l与圆C相交．
练习册系列答案
阅读快车系列答案
相关题目
