题目内容
在△ABC中,a、b、c分别为角A、B、C所对的边,且c=-3bcosA,tanC=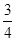 .
.
(1)求tanB的值;
(2)若c=2,求△ABC的面积.
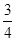 .
.(1)求tanB的值;
(2)若c=2,求△ABC的面积.
(1)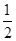 (2)
(2)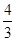
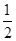 (2)
(2)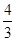
(1)由正弦定理,得sinC=-3sinBcosA,即sin(A+B)=-3sinBcosA.所以sinAcosB+cosAsinB=-3sinBcosA.
从而sinAcosB=-4sinBcosA.因为cosAcosB≠0,所以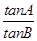 =-4.
=-4.
又tanC=-tan(A+B)=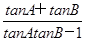 ,由(1)知,
,由(1)知,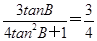 ,解得tanB=
,解得tanB=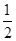 .
.
(2)由(1),得sinA= ,sinB=
,sinB=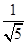 ,sinC=
,sinC=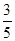 .
.
由正弦定理,得a= .
.
所以△ABC的面积为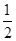 acsinB=
acsinB=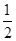 ×
×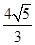 ×2×
×2×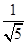 =
=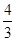
从而sinAcosB=-4sinBcosA.因为cosAcosB≠0,所以
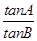 =-4.
=-4.又tanC=-tan(A+B)=
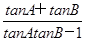 ,由(1)知,
,由(1)知,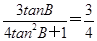 ,解得tanB=
,解得tanB=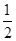 .
.(2)由(1),得sinA=
 ,sinB=
,sinB=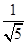 ,sinC=
,sinC=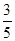 .
.由正弦定理,得a=
 .
.所以△ABC的面积为
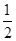 acsinB=
acsinB=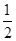 ×
×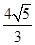 ×2×
×2×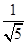 =
=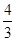

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
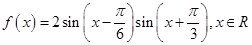 .
. 的最小正周期;
的最小正周期; 中,若
中,若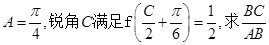 的值.
的值.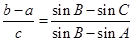 ,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.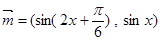 ,
, ,
,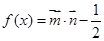 .
.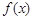 的单调递减区间;
的单调递减区间; 中,
中,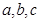 分别是角
分别是角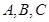 的对边,
的对边, ,
,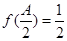 ,
, ,求
,求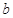 的大小.
的大小.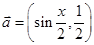 ,
,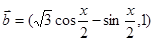 ,函数
,函数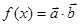 ,
, 三个内角
三个内角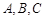 的对边分别为
的对边分别为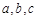 .
.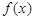 的单调递增区间;
的单调递增区间;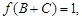
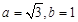 ,求
,求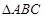 的面积
的面积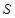 .
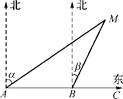
.
 .
.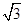 ,求a、b;
,求a、b;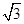 ,则S△ABC等于( )
,则S△ABC等于( )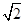 (B)
(B) 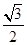 (D)2
(D)2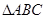 中,
中,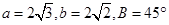 ,则
,则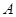 等于
等于