题目内容
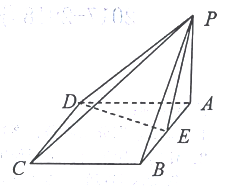
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP=AB=2，BC=2 
，E，F分别是AD，PC的中点．
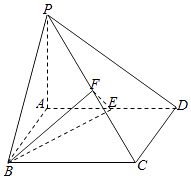
（1）证明：PC⊥平面BEF；
（2）求平面BEF与平面BAP所成的锐二面角的余弦值．
【答案】
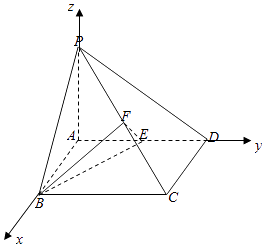
（1）证明：如图，以A为坐标原点，AB，AD，AP所在直线分别为x，y，z轴建立空间直角坐标系．
∵AP=AB=2，BC=AD=2 
，四边形ABCD是矩形，
∴A，B，C，D，P的坐标为A（0，0，0），B（2，0，0），
C（2，2 ，0），D（0，2 ，0），P（0，0，2）．
又E，F分别是AD，PC的中点，∴E（0， ，0），F（1， ，1）．
∴ 
=（2，2 ，﹣2）， 
=（﹣1， ，1）， 
=（1，0，1）．
∴ =﹣2+4﹣2=0， =2+0﹣2=0．
∴ ⊥ ， ⊥
∴PC⊥BF，PC⊥EF．又BF∩EF=F，
∴PC⊥平面BEF
（2）解：由（1）知平面BEF的一个法向量 
= =（2，2 ，﹣2），
平面BAP的一个法向量 
= 
=（0，2 ，0），∴ 
．
设平面BEF与平面BAP的夹角为θ，
则cosθ=|cos 
|= 
= 
= 
，
∴平面BEF与平面BAP所成的锐二面角的余弦值为 ．
【解析】（1）先建立适当的空间直角坐标系，再求得相关点的坐标，进而利用向量证明PC⊥BF，PC⊥EF，进而证得PC⊥平面BEF；（2）两个平面法向量所成夹角的余弦值的绝对值为这两个平面所成的锐二面角，故求得两平面的法向量即可解题.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．
