题目内容
已知圆M:x2+(y-2)2=1,设点B,C是直线l:x-2y=0上的两点,它们的横坐标分别是t,t+4(t∈R),点P在线段BC上,过P点作圆M的切线PA,切点为A.(1)若t=0,MP=
| 5 |
(2)经过A,P,M三点的圆的圆心是D,求线段DO长的最小值L(t).
分析:(1)由圆的方程找出圆心坐标与圆的半径,因为P在直线l上,所以设P的坐标为(a,2a),然后由M和P的坐标,利用两点间的距离公式表示出MP的长,根据MP=
列出关于a的方程,求出方程的解即可得到a的值,得到P的坐标,设过P点切线方程的斜率为k,根据P的坐标和斜率k写出切线的方程,根据直线与圆相切时圆心到直线的距离公式等于半径,利用点到直线的距离公式表示出圆心M到切线方程的距离d,让d等于圆的半径r,即可得到关于k的方程,求出方程的解即可得到k的值,写出直线PA的方程即可;
(2)根据圆的切线垂直于过切点的半径得到AP垂直AM,所以三角形APM为直角三角形,所以外接圆圆心D为斜边PM的中点,根据M和设出的P的坐标利用中点坐标公式表示出D的坐标,然后利用两点间的距离公式表示出OD的长,得到关于a的函数为开口向上的抛物线,分三种情况:
大于抛物线顶点的横坐标,
小于抛物线顶点的横坐标小于
+2,和
+2小于顶点的横坐标,利用二次函数的图象即可求出函数的最小值.线段DO长的最小值L(t)为一个分段函数,写出此分段函数的解析式即可.
| 5 |
(2)根据圆的切线垂直于过切点的半径得到AP垂直AM,所以三角形APM为直角三角形,所以外接圆圆心D为斜边PM的中点,根据M和设出的P的坐标利用中点坐标公式表示出D的坐标,然后利用两点间的距离公式表示出OD的长,得到关于a的函数为开口向上的抛物线,分三种情况:
| t |
| 2 |
| t |
| 2 |
| t |
| 2 |
| t |
| 2 |
解答:解:(1)由圆M:x2+(y-2)2=1,得到圆心M(0,2),半径r=1,
设P(2a,a)(0≤a≤2).
∵M(0,2),MP=
,∴
=
.
解得a=1或a=-
(舍去).
∴P(2,1).由题意知切线PA的斜率存在,设斜率为k.
所以直线PA的方程为y-1=k(x-2),即kx-y-2k+1=0.
∵直线PA与圆M相切,
∴
=1,
解得k=0或k=-
.
∴直线PA的方程是y=1或4x+3y-11=0;
(2)设f(a)min=f(
+2)=
(
+2)2+(
+2)+1=
t2+3t+8
∵PA与圆M相切于点A,∴PA⊥MA.
∴经过A,P,M三点的圆的圆心D是线段MP的中点.
∵M(0,2),∴D的坐标是(a,
+1).
设DO2=f(a).
∴f(a)=a2+(
+1)2=
a2+a+1=
(a+
)2+
.
当
>-
,即t>-
时,f(a)min=f(
)=
t2+
+1;
当
≤-
≤
+2,即-
≤t≤-
时,f(a)min=f(-
)=
;
当
+2<-
,即t<-
时,f(a)min=f(
+2)=
(
+2)2+(
+2)+1=
t2+3t+8
则L(t)=
.
设P(2a,a)(0≤a≤2).
∵M(0,2),MP=
| 5 |
| (2a)2+(a-2)2 |
| 5 |
解得a=1或a=-
| 1 |
| 5 |
∴P(2,1).由题意知切线PA的斜率存在,设斜率为k.
所以直线PA的方程为y-1=k(x-2),即kx-y-2k+1=0.
∵直线PA与圆M相切,
∴
| |-2-2k+1| | ||
|
解得k=0或k=-
| 4 |
| 3 |
∴直线PA的方程是y=1或4x+3y-11=0;
(2)设f(a)min=f(
| t |
| 2 |
| 5 |
| 4 |
| t |
| 2 |
| t |
| 2 |
| 15 |
| 16 |
∵PA与圆M相切于点A,∴PA⊥MA.
∴经过A,P,M三点的圆的圆心D是线段MP的中点.
∵M(0,2),∴D的坐标是(a,
| a |
| 2 |
设DO2=f(a).
∴f(a)=a2+(
| a |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
| 2 |
| 5 |
| 4 |
| 5 |
当
| t |
| 2 |
| 2 |
| 5 |
| 4 |
| 5 |
| t |
| 2 |
| 5 |
| 16 |
| t |
| 2 |
当
| t |
| 2 |
| 2 |
| 5 |
| t |
| 2 |
| 24 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
当
| t |
| 2 |
| 2 |
| 5 |
| 24 |
| 5 |
| t |
| 2 |
| 5 |
| 4 |
| t |
| 2 |
| t |
| 2 |
| 15 |
| 16 |
则L(t)=
|
点评:此题考查学生掌握直线与圆相切是所满足的条件,灵活运用两点间的距离公式及点到直线的距离公式化简求值,灵活运用二次函数求最值的方法解决实际问题,是一道比较难的题.

练习册系列答案
相关题目
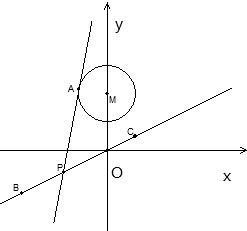 已知圆M:x2+(y-2)2=1,设点B,C是直线l:x-2y=0上的两点,它们的横坐标分别是t,t+4(t∈R),P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A
已知圆M:x2+(y-2)2=1,设点B,C是直线l:x-2y=0上的两点,它们的横坐标分别是t,t+4(t∈R),P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A