题目内容
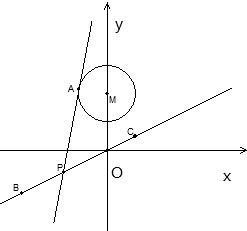 已知圆M:x2+(y-2)2=1,设点B,C是直线l:x-2y=0上的两点,它们的横坐标分别是t,t+4(t∈R),P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A
已知圆M:x2+(y-2)2=1,设点B,C是直线l:x-2y=0上的两点,它们的横坐标分别是t,t+4(t∈R),P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A(1)若t=0,MP=
| 5 |
(2)经过A,P,M三点的圆的圆心是D,
①将DO2表示成a的函数f(a),并写出定义域.
②求线段DO长的最小值.
分析:(1)设P(2a,a),由勾股定理结合题中数据建立关于a的方程,解之得a=1,得P(2,1).因此设直线PA的方程为y-1=k(x-2),利用点到直线的距离公式结合题意得出
=1,解之即可得到直线PA的方程;
(2)①由圆的性质结合PA与圆M相切,算出D的坐标(a,
+1),再利用两点的距离公式得到DO2关于a的二次函数表达式,从而得到DO2表示成a的函数f(a),并给出其定义域;
②根据二次函数的性质,得到f(a)min=f(
+2)=
t2+3t+8,再根据t<-
分三种情况加以讨论,分别结合二次函数的单调性求出最小值,最后综合可得线段DO的最小值关于a的分段形式的表达式,得到本题答案.
| |-2-2k+1| | ||
|
(2)①由圆的性质结合PA与圆M相切,算出D的坐标(a,
| a |
| 2 |
②根据二次函数的性质,得到f(a)min=f(
| t |
| 2 |
| 15 |
| 16 |
| 24 |
| 5 |
解答:解:(1)∵点B、C是直线l:x-2y=0上的两点,
∴可设P(2a,a)(0≤a≤2).
∵M(0,2),MP=
,∴
=
.
解得a=1或a=-
(舍去),可得P(2,1).
由题意知切线PA的斜率存在,设斜率为k.
可得直线PA的方程为y-1=k(x-2),即kx-y-2k+1=0.
∵直线PA与圆M相切,
∴
=1,解得k=0或k=-
.
因此直线PA的方程是y=1或4x+3y-11=0.
(2)①∵PA与圆M相切于点A,∴PA⊥MA.
∴经过A,P,M三点的圆的圆心D是线段MP的中点.
∵M(0,2),∴D的坐标是(a,
+1).
可得DO2=f(a)=a2+(
+1)2=
a2+a+1=
(a+
)2+
.(a∈[
,
])
②f(a)min=f(
+2)=
(
+2)2+(
+2)+1=
t2+3t+8(t<-
)
当
>-
,即t>-
时,f(a)min=f(
)=
t2+
+1;
当
≤-
≤
+2,即-
≤t≤-
时,f(a)min=f(-
)=
;
当
+2<-
,即t<-
时f(a)min=f(
+2)=
(
+2)2+(
+2)+1=
t2+3t+8
所以线段DO长的最小值为:L(t)=
.
∴可设P(2a,a)(0≤a≤2).
∵M(0,2),MP=
| 5 |
| (2a)2+(a-2)2 |
| 5 |
解得a=1或a=-
| 1 |
| 5 |
由题意知切线PA的斜率存在,设斜率为k.
可得直线PA的方程为y-1=k(x-2),即kx-y-2k+1=0.
∵直线PA与圆M相切,
∴
| |-2-2k+1| | ||
|
| 4 |
| 3 |
因此直线PA的方程是y=1或4x+3y-11=0.
(2)①∵PA与圆M相切于点A,∴PA⊥MA.
∴经过A,P,M三点的圆的圆心D是线段MP的中点.
∵M(0,2),∴D的坐标是(a,
| a |
| 2 |
可得DO2=f(a)=a2+(
| a |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
| 2 |
| 5 |
| 4 |
| 5 |
| t |
| 2 |
| t+4 |
| 2 |
②f(a)min=f(
| t |
| 2 |
| 5 |
| 4 |
| t |
| 2 |
| t |
| 2 |
| 15 |
| 16 |
| 24 |
| 5 |
当
| t |
| 2 |
| 2 |
| 5 |
| 4 |
| 5 |
| t |
| 2 |
| 5 |
| 16 |
| t |
| 2 |
当
| t |
| 2 |
| 2 |
| 5 |
| t |
| 2 |
| 24 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
当
| t |
| 2 |
| 2 |
| 5 |
| 24 |
| 5 |
| t |
| 2 |
| 5 |
| 4 |
| t |
| 2 |
| t |
| 2 |
| 15 |
| 16 |
所以线段DO长的最小值为:L(t)=
|
点评:本题给出直线与圆相切,求切线的方程并求线段长的最小值.着重考查了圆的方程、直线的方程、直线与圆的位置关系和二次函数的图象与性质等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目