题目内容
已知圆M:x2+(y-4)2=4,直线l的方程为x-2y=0,点P是直线l上一动点,过点P作圆的切线PA、PB,切点为A、B.
(Ⅰ)当P的横坐标为
时,求∠APB的大小;
(Ⅱ)求证:经过A、P、M三点的圆N必过定点,并求出所以定点的坐标.
(Ⅲ)求线段AB长度的最小值.
(Ⅰ)当P的横坐标为
| 16 | 5 |
(Ⅱ)求证:经过A、P、M三点的圆N必过定点,并求出所以定点的坐标.
(Ⅲ)求线段AB长度的最小值.
分析:(Ⅰ)由题可知,圆M的半径r=2,P(
,
),∠MAP=90°,根据MP=2r,可得∠MPA=30°,从而可求∠APB的大小;
(Ⅱ)设P的坐标,求出经过A、P、M三点的圆的方程即可得到圆过定点;
(Ⅲ)将圆N与圆M方程相减,可得圆M方程与圆N相交弦所在直线m方程,求出点M到直线m的距离,即可得到相交弦长,利用配方法,可求AB的最小值
.
| 16 |
| 5 |
| 8 |
| 5 |
(Ⅱ)设P的坐标,求出经过A、P、M三点的圆的方程即可得到圆过定点;
(Ⅲ)将圆N与圆M方程相减,可得圆M方程与圆N相交弦所在直线m方程,求出点M到直线m的距离,即可得到相交弦长,利用配方法,可求AB的最小值
| 11 |
解答:(Ⅰ)解:由题可知,圆M的半径r=2,P(
,
),
因为PA是圆M的一条切线,所以∠MAP=90°
又因MP=
=4=2r,
又∠MPA=30°,∠APB=60°; …(4分)
(Ⅱ)证明:设P(2b,b),因为∠MAP=90°,所以经过A、P、M三点的圆N以MP为直径,其方程为:(x-b)2+(y-
)2=
,即(2x+y-4)b-(x2+y2-4y)=0
由
,…(7分)
解得
或
,所以圆过定点(0,4),(
,
) …(9分)
(Ⅲ)解:因圆N方程为(x-b)2+(y-
)2=
即x2+y2-2bx-(b+4)y+4b=0 …①
圆M:x2+(y-4)2=4即x2+y2-8y+12=0 …②
②-①得圆M方程与圆N相交弦所在直线m方程为2bx+(b-4)y+12-4b=0…(11分)
点M到直线m的距离d=
…(13分)
相交弦长即AB=2
=4
=4
…(15分)
当b=
时,AB有最小值
…(17分)
| 16 |
| 5 |
| 8 |
| 5 |
因为PA是圆M的一条切线,所以∠MAP=90°
又因MP=
(0-
|
又∠MPA=30°,∠APB=60°; …(4分)
(Ⅱ)证明:设P(2b,b),因为∠MAP=90°,所以经过A、P、M三点的圆N以MP为直径,其方程为:(x-b)2+(y-
| b+4 |
| 2 |
| 4b2+(b-4)2 |
| 4 |
由
|
解得
|
|
| 8 |
| 5 |
| 4 |
| 5 |
(Ⅲ)解:因圆N方程为(x-b)2+(y-
| b+4 |
| 2 |
| 4b2+(b-4)2 |
| 4 |
圆M:x2+(y-4)2=4即x2+y2-8y+12=0 …②
②-①得圆M方程与圆N相交弦所在直线m方程为2bx+(b-4)y+12-4b=0…(11分)
点M到直线m的距离d=
| 4 | ||
|
相交弦长即AB=2
| 4-d2 |
1-
|
1-
|
当b=
| 4 |
| 5 |
| 11 |
点评:本题考查直线与圆的综合,考查圆过定点,考查圆的弦长问题,考查两圆位置关系,确定圆的方程是关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
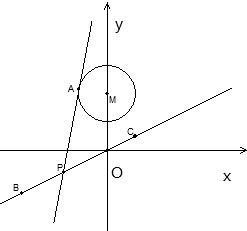 已知圆M:x2+(y-2)2=1,设点B,C是直线l:x-2y=0上的两点,它们的横坐标分别是t,t+4(t∈R),P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A
已知圆M:x2+(y-2)2=1,设点B,C是直线l:x-2y=0上的两点,它们的横坐标分别是t,t+4(t∈R),P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A