题目内容
已知圆M:x2+(y-2)2=1,定点A(4,2)在直线x-2y=0上,点P在线段OA上,过P点作圆M的切线PT,切点为T.(1)若MP=
| 5 |
(2)经过P,M,T三点的圆的圆心是D,求线段DO长的最小值L.
分析:(1)先由MP=
求得P 的坐标,根据圆心到切线的距离等于半径1,求得切线的斜率,点斜式求切线的方程.
(2)设P(2t,t),0≤t≤2,经过 P,M,T三点的圆的圆心为PM的中点D(t,1+
),求得OD2的解析式,利用二次函数的性质求得OD的最小值L.
| 5 |
(2)设P(2t,t),0≤t≤2,经过 P,M,T三点的圆的圆心为PM的中点D(t,1+
| t |
| 2 |
解答:解:(1)先由MP=
求得:P(2,1). 直线X=2与圆不相切,设直线PT:y-1=k(x-2),即:kx-y+1-2k=0,
圆心M(0,2)到直线距离为1,得:K=0 或k=-
,直线方程为:y=1或4x+3y-11=0.
(2)设P(2t,t),0≤t≤2,经过 P,M,T三点的圆的圆心为PM的中点D(t,1+
),
所以,OD2= t2+(1+
)2=
t2+t+1,0≤t≤2,t=0 时,得OD的最小值L=1.
| 5 |
圆心M(0,2)到直线距离为1,得:K=0 或k=-
| 4 |
| 3 |
(2)设P(2t,t),0≤t≤2,经过 P,M,T三点的圆的圆心为PM的中点D(t,1+
| t |
| 2 |
所以,OD2= t2+(1+
| t |
| 2 |
| 5 |
| 4 |
点评:本题考查用点斜式求直线的方程,直线和圆的位置关系,判断经过 P,M,T三点的圆的圆心为PM的中点D(t,1+
),是解题的难点和关键.
| t |
| 2 |

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
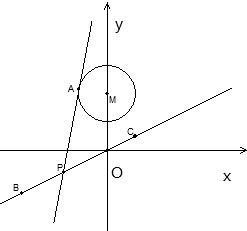 已知圆M:x2+(y-2)2=1,设点B,C是直线l:x-2y=0上的两点,它们的横坐标分别是t,t+4(t∈R),P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A
已知圆M:x2+(y-2)2=1,设点B,C是直线l:x-2y=0上的两点,它们的横坐标分别是t,t+4(t∈R),P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A