题目内容
【题目】(1)证明函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
(2)证明函数![]() 在(-π,0)上有且仅有一个极大值点
在(-π,0)上有且仅有一个极大值点![]() 且
且![]()
【答案】(1)见解析 (2)见解析
【解析】
(1)求出函数导数,根据导数正负性判断单调性即可证明.
(2)根据(1)已有信息,对函数进行二次求导,判断单调性及函数的零点,综合分析,再利用定义域计算函数值的取值范围,即可得证.
(1)对函数求导,得,
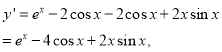
因为任意的![]() ,有
,有![]() ,且在区间
,且在区间![]() 上,
上,
![]()
所以![]()
即![]() ,
,
即函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
(2)对函数求导,得
![]() ,
,
令![]() ,则
,则![]()
当![]() 时,由(1)知,
时,由(1)知,![]() ,则
,则![]()
故![]() 在
在![]() 上单调递减
上单调递减
而![]()
由零点存在定理知:存在唯一的![]() ,使得
,使得![]() ,
,
即![]()
当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 为减函数.
为减函数.
又当![]() 时,
时,![]()
所以![]() 在
在![]() 上恒为减函数,
上恒为减函数,
因此![]() 有唯一的极大值点
有唯一的极大值点![]()
由![]() 在
在![]() 上单调递减,
上单调递减,
故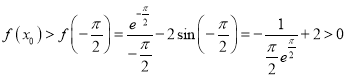
即![]()
又![]() 当
当![]() 时,
时,
![]()
故![]()
综上,函数![]() 在(-π,0)上有且仅有一个极大值点
在(-π,0)上有且仅有一个极大值点![]() 且
且![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】2020年2月1日0:00时,英国顺利“脱欧”.在此之前,英国“脱欧”这件国际大事被社会各界广泛关注,英国大选之后,曾预计将会在2020年1月31日完成“脱欧”,但是因为之前“脱欧”一直被延时,所以很多人认为并不能如期完成,某媒体随机在人群中抽取了100人做调查,其中40岁以上的55人中有10人认为不能完成,40岁以下的人中认为能完成的占![]() .
.
(1)完成![]() 列联表,并回答能否有90%的把握认为“预测国际大事的准确率与年龄有关”?
列联表,并回答能否有90%的把握认为“预测国际大事的准确率与年龄有关”?
能完成 | 不能完成 | 合计 | |
40岁以上 | |||
40岁以下 | |||
合计 |
(2)从上述100人中,采用按年龄分层抽样的方法,抽取20人,从这20人中再选取40岁以下的2人做深度调査,则2人中恰有1人认为英国能够完成“脱欧”的概率为多少?
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式为:
