题目内容
已知f(x)=ax3+bx2+cx+d为奇函数,且在点(2,f(2))处的切线方程为9x-y-16=0.
(1)求f(x)的解析式;
(2)若y=f(x)+m的图象与x轴仅有一个公共点,求m的范围.
(1)求f(x)的解析式;
(2)若y=f(x)+m的图象与x轴仅有一个公共点,求m的范围.
(1)∵f(x)为奇函数,∴b=d=0,∴f(x)=ax3+cx∵f(x)过点(2,2),f'(x)=3ax2+c,
∴
,
∴a=1,c=-3
∴f(x)=x3-3x(6分)
(2)设g(x)=f(x)+m,即g(x)=x3-3x+m,g'(x)=3x2-3=3(x+1)(x-1)
当x变化时,g'(x)变化情况如下表:
所以g'(x)的极大值2+m,极小值-2+m
要y=f(x)+m与x轴只有一个交点,只需-2+m>0或2+m<0
故当m∈(-∞,-2)∪(2,+∞)时,y=f(x)+m与x轴只有一个交点(13分).
∴
|
∴a=1,c=-3
∴f(x)=x3-3x(6分)
(2)设g(x)=f(x)+m,即g(x)=x3-3x+m,g'(x)=3x2-3=3(x+1)(x-1)
当x变化时,g'(x)变化情况如下表:
| x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
| g'(x) | + | 0 | - | 0 | + |
| g(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
要y=f(x)+m与x轴只有一个交点,只需-2+m>0或2+m<0
故当m∈(-∞,-2)∪(2,+∞)时,y=f(x)+m与x轴只有一个交点(13分).

练习册系列答案
相关题目
 在
在 中的最大值和最小值分别是( )
中的最大值和最小值分别是( )
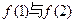


 的最小值为( )
的最小值为( )