题目内容
【题目】定义在R上的奇函数f(x),当x≥0时,f(x)= ![]() ,则关于x的函数F(x)=f(x)﹣a(0<a<1)的所有零点之和为( )
,则关于x的函数F(x)=f(x)﹣a(0<a<1)的所有零点之和为( )
A.3a﹣1
B.1﹣3a
C.3﹣a﹣1
D.1﹣3﹣a
【答案】B
【解析】解:∵定义在R上的奇函数f(x), ∴f(﹣x)=﹣f(x),
∵当x≥0时,f(x)= ![]() ,
,
∴当x≥0时,f(x)= 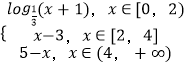 ,
,
得出x<0时,f(x)= ![]()
画出图象得出: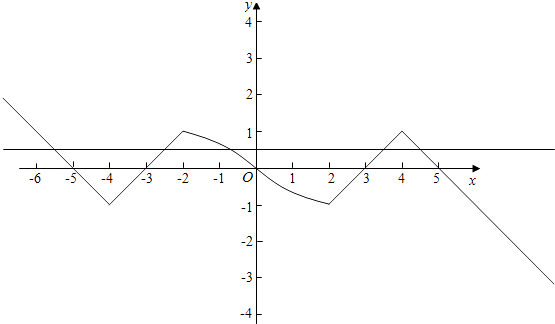
如图从左向右零点为x1 , x2 , x3 , x4 , x5 ,
根据对称性得出:x1+x2=﹣4×2=﹣8,
x4+x5=2×4=8,﹣log ![]() (﹣x3+1)=a,x3=1﹣3a ,
(﹣x3+1)=a,x3=1﹣3a ,
故x1+x2+x3+x4+x5=﹣8+1﹣3a+8=1﹣3a ,
故选:B
【考点精析】掌握函数的零点与方程根的关系是解答本题的根本,需要知道二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目