题目内容
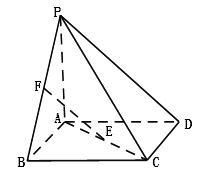
【题目】如图,四棱锥 ![]() 的底面
的底面 ![]() 为正方形,
为正方形, ![]() ⊥底面
⊥底面 ![]() ,
, ![]() 分别是
分别是 ![]() 的中点,
的中点, ![]() .
.
(Ⅰ)求证 ![]() ∥平面
∥平面 ![]() ;
;
(Ⅱ)求直线 ![]() 与平面
与平面 ![]() 所成的角;
所成的角;
(Ⅲ)求四棱锥 ![]() 的外接球的体积.
的外接球的体积.
【答案】解:(Ⅰ)如图,连结 ![]() ,则
,则 ![]() 是
是 ![]() 的中点,又
的中点,又 ![]() 是
是 ![]() 的中点,
的中点,
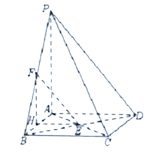
∴ ![]() .又∵
.又∵ ![]() 平面
平面 ![]() ,
, ![]() 面
面 ![]()
∴ ![]() 平面
平面 ![]() .
.
(Ⅱ)取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() .
.
在正方形 ![]() 中,
中, ![]() 是
是 ![]() 的中点,有
的中点,有 ![]() .
.
∵ ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,∴
,∴ ![]() ,
,
∵ ![]() ,∴
,∴ ![]() 平面
平面 ![]() ,
,
∴ ![]() 是直线
是直线 ![]() 在平面
在平面 ![]() 的射影,∴
的射影,∴ ![]() 是直线
是直线 ![]() 与平面
与平面 ![]() 所成的角,
所成的角,
在直角三角形 ![]() 中,
中, ![]() ,所以
,所以 ![]() .
.
∴直线 ![]() 与平面
与平面 ![]() 所成的角为45°.
所成的角为45°.
(Ⅲ)设四棱锥 ![]() 的外接球半径为
的外接球半径为 ![]() ,
, ![]() ,则
,则
![]() ,即
,即 ![]() .
.
所以外接球的体积为 ![]() ..
..
【解析】(1)根据题意作出辅助线,利用线面平行的判定定理即可得证。(2)由题意结合线面垂直的判断定理可得证H E ⊥ 平面 P A B,进而找出二面角的平面角结合题中已知在直角三角形中求出线面角即可。(3)根据题意把四棱锥补成为一个球内接长方体,球的直径为长方体的体对角线进而求出半径再结合球的体积公式代入数值求出即可。
【考点精析】本题主要考查了直线与平面平行的性质和直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目