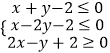题目内容
【题目】若
的部分图象如图所示.
（1）求函数
的解析式；
（2）将
的图象向左平移
个单位长度得到
的图象，若
图象的一个对称轴为
，求
的最小值；
（3）在第（2）问的前提下，求函数
在
上的单调区间.
【答案】（1）
（2）
（3）单增区间为
，单减区间为
.
【解析】试题分析：（1）由函数的图象的顶点坐标求出
，由周期求出
，由五点法作图求出
的值，可得函数的解析式；（2）根据平移原则得
，令
结合
的范围得结果；（3）根据（2）中的结果，解不等式
，结合
的范围，可求单调增区间，余下即为减区间.
试题解析：（1）由图知周期
，∴
且A=2，
∴
，把
，y=0代入上式得
，
∴
，即
.
又
，∴
.即
.
（2）
，
由题意得： 
，∴
，
∵
，∴当k=2时， 
的最小值为
.
（3）此时
，令
，解得
，结合
，得
，于是函数
在
上的单增区间为
，单减区间为
.
练习册系列答案
相关题目
