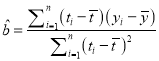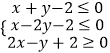Question

【题目】已知椭圆 的离心率为 ，且经过点 是椭圆的左、右焦点.
（1）求椭圆 的方程；
（2）点 在椭圆上运动，求 的最大值.

Answer 1

【答案】
（1）解：由题意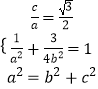，得 ，解得

所以椭圆 的方程为

（2）解：由均值定理 ，

又 ，

所以 ，当且仅当 时等号成立.

所以 得最大值为4.

【解析】(1)由已知列出关于a、b、c的方程组，求解方程组可得a、b、c的值进而得出椭圆的方程。(2)根据题意由椭圆的定义可求出a的值，再结合基本不等式的性质求出的最大值。
【考点精析】本题主要考查了基本不等式在最值问题中的应用和椭圆的概念的相关知识点，需要掌握用基本不等式求最值时（积定和最小，和定积最大），要注意满足三个条件“一正、二定、三相等”；平面内与两个定点，的距离之和等于常数（大于）的点的轨迹称为椭圆,这两个定点称为椭圆的焦点，两焦点的距离称为椭圆的焦距才能正确解答此题．