题目内容
已知F1、F2为双曲线C:
-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则P到x轴的距离为( )
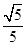-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则P到x轴的距离为( )A． | B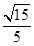． | C． | D． |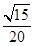
B
由双曲线的方程可知a=2,b=1,c=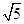
,
在△F1PF2中,根据余弦定理可得
(2c)2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos60°,
即4c2=(|PF1|-|PF2|)2+|PF1|·|PF2|,
所以4c2=4a2+|PF1|·|PF2|,
所以|PF1|·|PF2|=4c2-4a2=20-16=4,
所以△F1PF2的面积为S=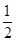
|PF1|·|PF2|sin60°
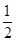=×4×
=
,
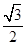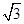设△F1PF2边F1F2上的高为h,
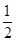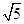则S=×2chh=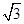,所以高h=
=,
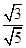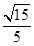即点P到x轴的距离为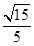.故选B.
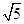,在△F1PF2中,根据余弦定理可得
(2c)2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos60°,
即4c2=(|PF1|-|PF2|)2+|PF1|·|PF2|,
所以4c2=4a2+|PF1|·|PF2|,
所以|PF1|·|PF2|=4c2-4a2=20-16=4,
所以△F1PF2的面积为S=
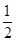|PF1|·|PF2|sin60°=
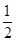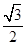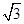×4×=,设△F1PF2边F1F2上的高为h,
则S=
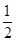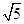×2chh=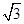,所以高h=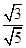=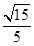,即点P到x轴的距离为
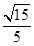.故选B.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
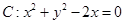的圆心到双曲线
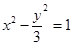的渐近线的距离是（ ）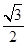
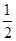
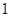
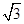
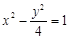有共同的渐近线,且经过点P(1,4)的双曲线方程为 （ ）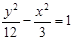
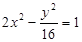
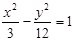
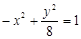
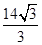,且∠ABC=120°,BC=10,边BC在x轴上且y轴垂直平分BC边,则过点A且以B,C为焦点的双曲线方程为( )
-
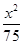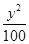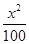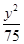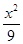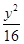=1
-
=1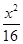
-
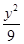=1
-
=1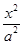
-
=1(a>0,b>0)的离心率为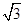
,则双曲线的渐近线方程为( )
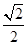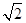x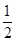
x
x
,则双曲线C1:
-
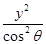=1与C2: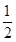
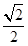
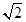
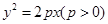的焦点F恰好是双曲线
的右焦点，且两条曲线的交点的连线过点F，则该双曲线的离心率为（ ）
+1