题目内容
(12分)(2011•陕西)如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把是BC上的△ABD折起,使∠BDC=90°.

(Ⅰ)证明:平面ADB⊥平面BDC;
(Ⅱ)设BD=1,求三棱锥D﹣ABC的表面积.

(Ⅰ)证明:平面ADB⊥平面BDC;
(Ⅱ)设BD=1,求三棱锥D﹣ABC的表面积.
(Ⅰ)见解析(Ⅱ)

试题分析:(Ⅰ)翻折后,直线AD与直线DC、DB都垂直,可得直线与平面BDC垂直,再结合AD是平面ADB内的直线,可得平面ADB与平面垂直;
(Ⅱ)根据图形特征可得△ADB、△DBC、△ADC是全等的等腰直角三角形,△ABC是等边三角形,利用三角形面积公式可得三棱锥D﹣ABC的表面积.
解:(Ⅰ)∵折起前AD是BC边上的高,
∴当△ABD折起后,AD⊥DC,AD⊥DB,
又DB∩DC=D,
∴AD⊥平面BDC,
∵AD?平面ABD.
∴平面ADB⊥平面BDC
(Ⅱ)由(Ⅰ)知,DA⊥DB,DB⊥DC,DC⊥DA,
∵DB=DA=DC=1,∴AB=BC=CA=
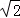 ,
,从而
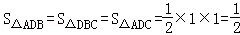
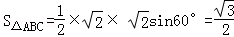
所以三棱锥D﹣ABC的表面积为:

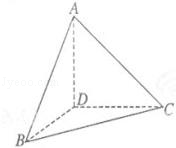
点评:解决平面图形翻折问题的关键是看准翻折后没有发生变化的位置关系,抓住翻折后仍然垂直的直线作为条件,从而解决问题.

练习册系列答案
相关题目
 ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点. 平面
平面 ;(2)(2)求此几何体的体积.
;(2)(2)求此几何体的体积.
 中,
中, ,
, ,
, °,平面
°,平面 平面
平面 ,
, ,
, 分别为
分别为 ,
, 中点.
中点. ∥平面
∥平面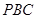 ;
;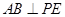 ;
; 的体积.
的体积.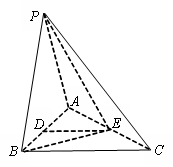





 ,则原四边形的面积是多少?
,则原四边形的面积是多少?
 时,则该圆锥体的体积是 .
时,则该圆锥体的体积是 . ,它的三视图中的俯视图如图所示,侧视图是一个矩形,则这个矩形的面积是( )
,它的三视图中的俯视图如图所示,侧视图是一个矩形,则这个矩形的面积是( )
