题目内容
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4, ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点.
(1)求证:平面AHC 平面
平面 ;(2)(2)求此几何体的体积.
;(2)(2)求此几何体的体积.
 ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点.(1)求证:平面AHC
 平面
平面 ;(2)(2)求此几何体的体积.
;(2)(2)求此几何体的体积.
(1)详见解析;(2) .
.
 .
.试题分析:(1)要证面面垂直,首先证线面垂直.那么在本题中证哪条线垂直哪个面?结合条件可得
 ,
, ,所以
,所以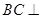 面AHC,从而平面AHC
面AHC,从而平面AHC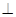 平面BCE.(2)可将该几何体切割为三部分:
平面BCE.(2)可将该几何体切割为三部分: ,然后分别求出三部分的体积相加即得.
,然后分别求出三部分的体积相加即得.(1)在菱形ABEF中,因为
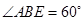 ,所以
,所以 是等边三角形,又因为H是线段EF的中点,所以
是等边三角形,又因为H是线段EF的中点,所以
因为面ABEF
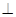 面ABCD,且面ABEF
面ABCD,且面ABEF 面ABCD=AB,
面ABCD=AB,所以AH
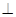 面ABCD,所以
面ABCD,所以
在直角梯形中,AB=2AD=2CD=4,
 ,得到
,得到 ,从而
,从而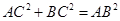 ,所以
,所以 ,又AH
,又AH AC=A
AC=A所以
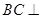 面AHC,又
面AHC,又 面BCE,所以平面AHC
面BCE,所以平面AHC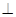 平面BCE .6分
平面BCE .6分(2)因为
 ,
,
所以
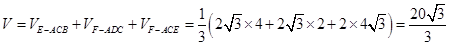 .12分
.12分
练习册系列答案
相关题目
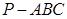 ,其表面展开图是三角形
,其表面展开图是三角形 ,如图,求△
,如图,求△ .
.

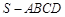 中,
中,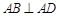 ,
,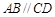 ,
,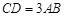 ,平面
,平面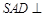 平面
平面 ,
,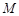 是线段
是线段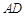 上一点,
上一点,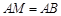 ,
,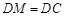 ,
,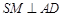 .
.
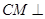
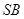 ;
;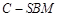 与四棱锥
与四棱锥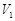 与
与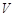 ,求
,求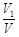 的值.
的值.
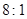 ,则它们的表面积之比为( )
,则它们的表面积之比为( )


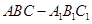 的底面边长为
的底面边长为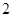 ,侧棱长为
,侧棱长为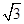 ,
,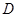 为
为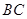 中点,则三棱锥
中点,则三棱锥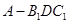 的体积为
的体积为



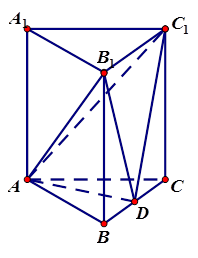
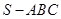 的四个顶点都在球面上,SA是球的直径,
的四个顶点都在球面上,SA是球的直径,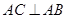 ,
, ,则该球的表面积为( )
,则该球的表面积为( )



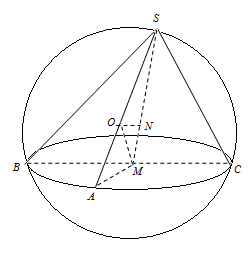
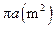 ,且它的侧面展开图是一个半圆,则圆锥的底面半径为 .
,且它的侧面展开图是一个半圆,则圆锥的底面半径为 .