题目内容
【题目】已知椭圆![]() (
(![]() )的焦点分别为
)的焦点分别为![]() ,
,![]() ,离心率
,离心率![]() ,过左焦点的直线与椭圆交于
,过左焦点的直线与椭圆交于![]() ,
,![]() 两点,
两点,![]() ,且
,且![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() 与椭圆有两个不同的交点
与椭圆有两个不同的交点![]() ,
,![]() ,且点
,且点![]() 在点
在点![]() ,
,![]() 之间,试求
之间,试求![]() 和
和![]() 面积之比的取值范围(其中
面积之比的取值范围(其中![]() 为坐标原点).
为坐标原点).
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)先根据正弦定理将角化为边![]() ,再根据椭圆定义得
,再根据椭圆定义得![]() ,求得
,求得![]() ,根据离心率求得
,根据离心率求得![]() ,
,![]() ,(2)两面积之比等于A,B两点纵坐标之比,所以先设
,(2)两面积之比等于A,B两点纵坐标之比,所以先设![]() 的方程为
的方程为![]() ,与椭圆方程联立方程组,结合韦达定理得
,与椭圆方程联立方程组,结合韦达定理得![]() ,令
,令![]() ,消元可得
,消元可得![]() ,即
,即![]() . 根据判别式大于零得
. 根据判别式大于零得![]() .解不等式可得
.解不等式可得![]() 取值范围
取值范围
试题解析:(Ⅰ)在![]() 中,由正弦定理得
中,由正弦定理得![]() ,由椭圆定义得
,由椭圆定义得![]() ,所以
,所以![]() ,故
,故![]() ,又
,又![]() ,所以
,所以![]() ,
,![]() ,所以椭圆的标准方程为
,所以椭圆的标准方程为![]() .
.
(Ⅱ)依题意知直线![]() 的斜率存在且不为0,设
的斜率存在且不为0,设![]() 的方程为
的方程为![]() ,与椭圆方程
,与椭圆方程![]() 联立,
联立,
消去x整理得![]() ,
,
由![]() ,解得
,解得![]() .
.
设![]() ,则
,则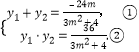
令![]() ,则
,则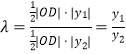 ,且
,且![]() .
.
将![]() 代人①②得
代人①②得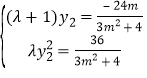 ,消去
,消去![]() 得
得![]() ,
,
即![]() .
.
由![]() ,得
,得![]() ,所以
,所以![]() 且
且![]() ,
,
解得![]() 或
或![]() .
.
又![]() ,∴
,∴![]() ,故
,故![]() 和
和![]() 面积之比的取值范围为
面积之比的取值范围为![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值
为![]() ,当
,当![]() 时,产品为一级品;当
时,产品为一级品;当![]() 时,产品为二级品,当
时,产品为二级品,当![]() 时,产品为三级品,现用两种新配方(分别称为
时,产品为三级品,现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做实验,各生产了100件这种产品,
配方)做实验,各生产了100件这种产品,
并测量了每件产品的质量指标值,得到下面的试验结果:(以下均视频率为概率)
![]() 配方的频数分配表
配方的频数分配表
指标值分组 |
|
|
|
|
频数 | 10 | 30 | 40 | 20 |
![]() 配方的频数分配表
配方的频数分配表
指标值分组 |
|
|
|
|
|
频数 | 5 | 10 | 15 | 40 | 30 |
(Ⅰ)若从![]() 配方产品中有放回地随机抽取3件,记“抽出的
配方产品中有放回地随机抽取3件,记“抽出的![]() 配方产品中至少1件二级品”为事件
配方产品中至少1件二级品”为事件![]() ,求事件
,求事件![]() 发生的概率
发生的概率![]() ;
;
(Ⅱ)若两种新产品的利润率![]() 与质量指标
与质量指标![]() 满足如下关系:
满足如下关系: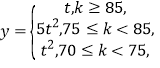 其中
其中![]() ,从长期来看,投资哪种配方的产品平均利润率较大?
,从长期来看,投资哪种配方的产品平均利润率较大?


