Question

【题目】已知O为坐标原点，对于函数，称向量为函数的伴随向量，同时称函数为向量的伴随函数.

（1）设函数，试求的伴随向量；

（2）记向量的伴随函数为，求当且时的值；

（3）由（1）中函数的图象（纵坐标不变）横坐标伸长为原来的2倍，再把整个图象向右平移个单位长度得到的图象，已知，，问在的图象上是否存在一点P，使得.若存在，求出P点坐标；若不存在，说明理由.

Answer 1

【答案】（1）（2）（3）存在，

【解析】

(1)利用三角函数诱导公式化简函数得，根据题意写出伴随向量； (2)根据题意求出函数，再由及求出及，由展开代入相应值即可得解；(3) 根据三角函数图像变换规则求出的解析式，设，由得列出方程求出满足条件的点P的坐标即可.

（1）∵

∴

∴的伴随向量

（2）向量的伴随函数为，

，

，

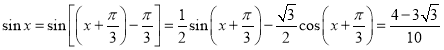
（3）由（1）知：

将函数的图像（纵坐标不变）横坐标伸长为原来的2倍，得到函数

再把整个图像向右平移个单位长得到的图像，得到

设，∵

∴，

又∵，∴

∴

∴（*）

∵，∴

∴

又∵

∴当且仅当时，和同时等于，这时（*）式成立

∴在的图像上存在点，使得.