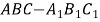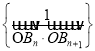题目内容
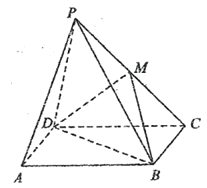
【题目】如图，在四棱锥P—ABCD中，四边形ABCD是矩形，平面PCD⊥平面ABCD，M为PC中点．求证：
（1）PA∥平面MDB；
（2）PD⊥BC．
【答案】（1）详见解析；（2）详见解析.
【解析】
试题分析：（1）线面平行的判定关键在证相应线线平行，线线平行的证明或寻求需要结合平面几何的知识，如中位线平行于底面，因为本题中M为PC中点，所以应取BD的中点作为解题突破口；（2）线线垂直的证明一般需要经过多次线线垂直与线面垂直的转化，而对于面面垂直，基本是单向转化，即作为条件，就将其转化为线面垂直；作为结论，只需寻求线面垂直.如本题中面PCD与面ABCD垂直，就转化为BC
平面PCD，到此所求问题转化为:已知线面垂直，要求证线线垂直.在线线垂直与线面垂直的转化过程中，要注意充分应用平面几何中的垂直条件,如矩形邻边相互垂直.
试题解析：证明：（1）连结AC交BD于点O,连结OM. 2分
因为M为PC中点,O为AC中点，
所以MO//PA. 4分
因为MO
平面MDB，PA
平面MDB,
所以PA//平面MDB. 7分
（2）因为平面PCD平面ABCD,
平面PCD
平面ABCD =CD,
BC平面ABCD ,BCCD,
所以BC平面PCD. 12分
因为PD平面PCD,
所以BCPD 14分
【题目】某企业为确定下一年投入某种产品的研发费用，需了解年研发费用
（单位：千万元）对年销售量
（单位：千万件）的影响，统计了近
年投入的年研发费用
与年销售量
的数据，得到散点图如图所示．
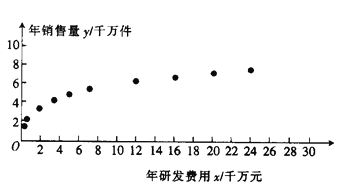
(1)利用散点图判断
和
（其中
均为大于
的常数）哪一个更适合作为年销售量和年研发费用的回归方程类型（只要给出判断即可，不必说明理由）
(2)对数据作出如下处理，令
，得到相关统计量的值如下表：根据第(1)问的判断结果及表中数据，求关于的回归方程；
|
|
|
|
15 | 15 | 28.25 | 56.5 |
(3)已知企业年利润
（单位：千万元）与的关系为
（其中
），根据第(2)问的结果判断，要使得该企业下一年的年利润最大，预计下一年应投入多少研发费用?
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为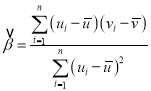
，
