题目内容
四棱锥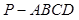 的底面
的底面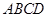 是正方形,侧棱
是正方形,侧棱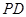 ⊥底面
⊥底面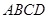 ,
,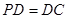 ,
,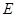 是
是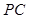 的中点.
的中点.
(Ⅰ)证明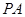 //平面
//平面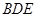 ;
;
(Ⅱ)求二面角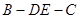 的平面角的余弦值;
的平面角的余弦值;
(Ⅲ)在棱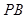 上是否存在点
上是否存在点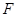 ,使
,使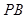 ⊥平面
⊥平面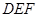 ?若存在,请求出
?若存在,请求出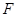 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.
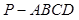 的底面
的底面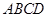 是正方形,侧棱
是正方形,侧棱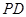 ⊥底面
⊥底面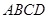 ,
,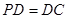 ,
,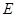 是
是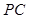 的中点.
的中点. (Ⅰ)证明
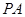 //平面
//平面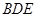 ;
; (Ⅱ)求二面角
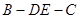 的平面角的余弦值;
的平面角的余弦值;(Ⅲ)在棱
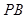 上是否存在点
上是否存在点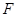 ,使
,使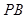 ⊥平面
⊥平面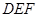 ?若存在,请求出
?若存在,请求出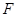 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.(1)见解析;(2)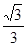 ;(3)棱
;(3)棱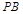 上存在点
上存在点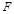 ,
,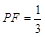
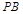 ,使得
,使得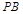 ⊥平面
⊥平面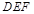 。
。
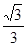 ;(3)棱
;(3)棱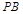 上存在点
上存在点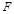 ,
,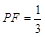
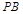 ,使得
,使得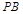 ⊥平面
⊥平面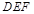 。
。解:(Ⅰ)以 为坐标原点,分别以
为坐标原点,分别以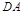 、
、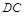 、
、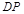 所在直线为x轴、y轴、z轴建立空间直角坐标系 设PD=DC=2,则A(2,0,0),P(0,0,2),E(0,1,1),
所在直线为x轴、y轴、z轴建立空间直角坐标系 设PD=DC=2,则A(2,0,0),P(0,0,2),E(0,1,1),
B(2,2,0).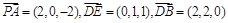
设 是平面BDE的一个法向量,
是平面BDE的一个法向量,
则由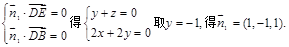

(II)由(Ⅰ)知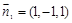 是平面
是平面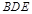 的一个法向量,
的一个法向量,
又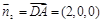 是平面
是平面 的一个法向量.
的一个法向量.
设二面角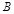 -
-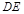 -
-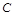 的平面角为
的平面角为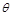 ,由图可知
,由图可知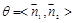
∴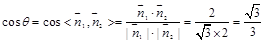
故二面角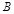 -
-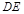 -
-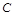 的余弦值为
的余弦值为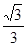
(Ⅲ)∵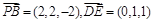 ∴
∴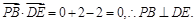
假设棱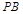 上存在点
上存在点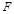 ,使
,使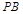 ⊥平面
⊥平面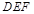 ,设
,设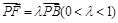 ,
,
则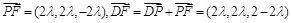 ,
,
由
∴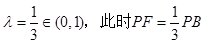
即在棱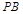 上存在点
上存在点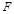 ,
,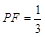
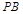 ,使得
,使得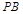 ⊥平面
⊥平面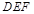 。
。
 为坐标原点,分别以
为坐标原点,分别以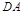 、
、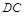 、
、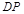 所在直线为x轴、y轴、z轴建立空间直角坐标系 设PD=DC=2,则A(2,0,0),P(0,0,2),E(0,1,1),
所在直线为x轴、y轴、z轴建立空间直角坐标系 设PD=DC=2,则A(2,0,0),P(0,0,2),E(0,1,1),B(2,2,0).
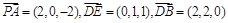
设
 是平面BDE的一个法向量,
是平面BDE的一个法向量,则由
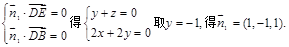

(II)由(Ⅰ)知
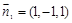 是平面
是平面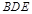 的一个法向量,
的一个法向量,又
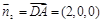 是平面
是平面 的一个法向量.
的一个法向量. 设二面角
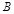 -
-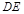 -
-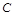 的平面角为
的平面角为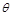 ,由图可知
,由图可知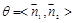
∴
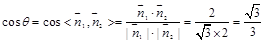
故二面角
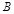 -
-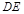 -
-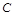 的余弦值为
的余弦值为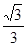
(Ⅲ)∵
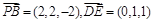 ∴
∴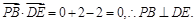
假设棱
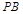 上存在点
上存在点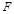 ,使
,使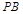 ⊥平面
⊥平面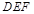 ,设
,设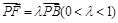 ,
,则
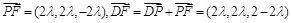 ,
,由

∴
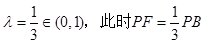
即在棱
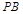 上存在点
上存在点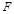 ,
,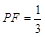
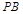 ,使得
,使得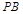 ⊥平面
⊥平面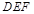 。
。
练习册系列答案
相关题目
 面ABC,BC
面ABC,BC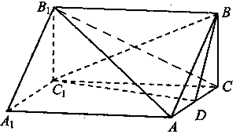
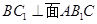 ;
;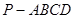 中,
中,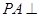 平面
平面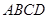 ,底面
,底面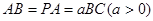 .
.
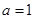 时,求证:
时,求证: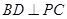 ;
;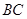 边上有且只有一个点
边上有且只有一个点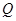 ,使得
,使得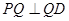 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.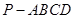 的底面
的底面 是矩形,
是矩形,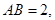
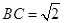 ,且侧面
,且侧面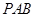 是正三角形,平面
是正三角形,平面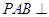 平面
平面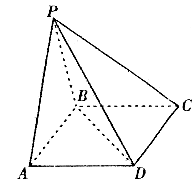
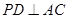 ;
;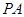 上是否存在一点
上是否存在一点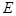 ,使得二面角
,使得二面角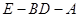 的大小为45°.若存在,试求
的大小为45°.若存在,试求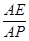 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.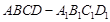 中,
中,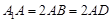 ,
,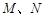 分别是
分别是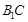 、
、 中点。
中点。 ;
;  的正切值。
的正切值。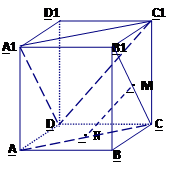
 、
、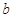 、
、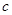 表示三条不同的直线,
表示三条不同的直线,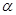 表示平面,给出下列命题:
表示平面,给出下列命题: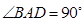 ,AD∥BC, AB="BC=2," AD="4,"
,AD∥BC, AB="BC=2," AD="4," 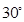 角,E是PD的中点.
角,E是PD的中点. 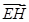 的坐标;
的坐标;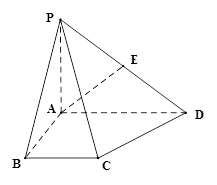
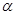 、
、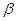 是两个不同的平面,则下列说法正确的是
是两个不同的平面,则下列说法正确的是