题目内容
【题目】如果数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等差数列”,
是“间等差数列”,![]() 为“间公差”.若数列
为“间公差”.若数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求证:数列![]() 是“间等差数列”,并求间公差
是“间等差数列”,并求间公差![]() ;
;
(2)设![]() 为数列
为数列![]() 的前n项和,若
的前n项和,若![]() 的最小值为-153,求实数
的最小值为-153,求实数![]() 的取值范围;
的取值范围;
(3)类似地:非零数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等比数列”,
是“间等比数列”,![]() 为“间公比”.已知数列
为“间公比”.已知数列![]() 中,满足
中,满足![]() ,
,![]() ,
,![]() ,试问数列
,试问数列![]() 是否为“间等比数列”,若是,求最大的整数
是否为“间等比数列”,若是,求最大的整数![]() 使得对于任意
使得对于任意![]() ,都有
,都有![]() ;若不是,说明理由.
;若不是,说明理由.
【答案】(1)见解析;(2)![]() ;(3)63.
;(3)63.
【解析】
(1)直接利用定义求出数列为间等差数列.
(2)利用分类讨论思想,利用数列的前n项和公式求出数列的和,进一步利用不等量关系求出结果.
(3)利用分类讨论思想,进一步求出数列的通项公式,再利用函数的单调性求出k的最大值.
(1)若数列{an}满足an+an+1=2n﹣35,n∈N*,则:an+1+an+2=2(n+1)﹣35,
两式相减得:an+2﹣an=2.故数列{an}是“间等差数列”,公差d=2.
(2)(i)当n=2k时,
![]() (a1+a2)+(a3+a4)+…+(an﹣1+an)=﹣33﹣29+…+(2n﹣37)=
(a1+a2)+(a3+a4)+…+(an﹣1+an)=﹣33﹣29+…+(2n﹣37)=![]()
易知:当n=18时,最小值S18=﹣153.
(ii)当n=2k+1时,
Sn=a1+(a2+a3)+(a4+a5)+…+(an﹣1+an)=a1+(﹣31)+(﹣29)+…+(2n﹣37)=![]() ,
,
当n=17时最小,其最小值为S17=a﹣136,要使其最小值为﹣153,
则:a﹣136≥﹣153,解得:a≥﹣17.
(3)易知:cncn+1=2018(![]() )n﹣1,则:cn+1cn+2=2018(
)n﹣1,则:cn+1cn+2=2018(![]() )n,
)n,
两式相除得:![]() ,故数列{cn}为“间等比数列”,其间等比为
,故数列{cn}为“间等比数列”,其间等比为![]() .
.![]() ,
,
易求出数列的通项公式为: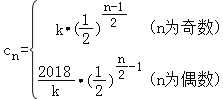 ,
,
由于![]() n>
n>![]() n+1,则数列{
n+1,则数列{![]() n}单调递减.那么,奇数项和偶数项都为单调递减,所以:k>0.
n}单调递减.那么,奇数项和偶数项都为单调递减,所以:k>0.
要使数列为单调递减数列.只需![]() 2m﹣1>
2m﹣1>![]() 2m>
2m>![]() 2m+1,
2m+1,
即:![]() ,
,
解得![]() ,即最大的整数
,即最大的整数![]() .
.