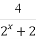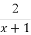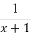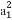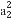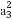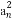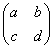题目内容
等差数列{an}中,2a1+3a2=11,2a3=a2+a6-4,其前n项和为Sn.
(1)求数列{an}的通项公式.
(2)设数列{bn}满足bn=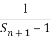 ,其前n项和为Tn,求证:Tn<
,其前n项和为Tn,求证:Tn< (n∈N*).
(n∈N*).
(1) an=2n-1 (2)见解析
【解析】(1)2a1+3a2=2a1+3(a1+d)=5a1+3d=11,
2a3=a2+a6-4,
即2(a1+2d)=a1+d+a1+5d-4,得d=2,
则a1=1,故an=2n-1.
(2)由(1)得Sn=n2,∴bn=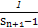 =
=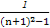
=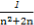 =
=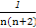 =
=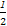 (
(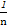 -
- ),
),
Tn=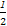 (
(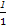 -
-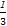 +
+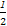 -
-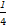 +
+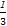 -
-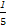 +…+
+…+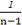 -
-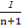 +
+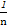 -
- )
)
=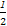 (
(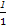 +
+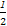 -
-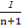 -
- )<
)<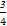 (n∈N*).
(n∈N*).
【方法技巧】裂项相消法的应用技巧
裂项相消法的基本思想是把数列的通项an分拆成an=bn+1-bn或者an=bn-bn+1或者an=bn+2-bn等,从而达到在求和时逐项相消的目的,在解题中要善于根据这个基本思想变换数列an的通项公式,使之符合裂项相消的条件.在裂项时一定要注意把数列的通项分拆成的两项一定是某个数列中的相邻的两项或者是等距离间隔的两项,只有这样才能实现逐项相消后剩下几项,达到求和的目的.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目