题目内容
【题目】已知![]() ,
,![]() ,对任意
,对任意![]() ,有
,有![]() 成立.
成立.
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,求正整数
项和,求正整数![]() ,使得对任意
,使得对任意![]() ,
,![]() 恒成立;
恒成立;
(3)设![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,若对任意
项和,若对任意![]() 均有
均有![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]() 或
或![]() (3)
(3)![]()
【解析】
(1)由![]() 可得
可得![]() ,结合平面向量的坐标运算可得到
,结合平面向量的坐标运算可得到![]() 的关系式,再结合
的关系式,再结合![]() 可证明数列
可证明数列![]() 是等比数列,进而可求出通项公式;
是等比数列,进而可求出通项公式;
(2)将![]() 两端同时除以
两端同时除以![]() ,可得到
,可得到![]() ,从而可证明数列
,从而可证明数列![]() 是等差数列,即可求出
是等差数列,即可求出![]() 的表达式,进而求得
的表达式,进而求得![]() 的通项公式,通过判断其表达式特点,可求出满足题意的正整数
的通项公式,通过判断其表达式特点,可求出满足题意的正整数![]() ;
;
(3)由题得,![]() ,利用裂项相消求和法可求出
,利用裂项相消求和法可求出![]() ,结合不等式的性质,可求出
,结合不等式的性质,可求出![]() 的最小值.
的最小值.
(1)由题可得![]() ,则
,则![]() ,
,
当![]() 时,可得
时,可得![]() .
.
![]() 时,
时,![]() ,则
,则![]() ,即
,即![]() ,
,
故数列![]() 是以2为首项,公比为2的等比数列,通项公式为
是以2为首项,公比为2的等比数列,通项公式为![]() .
.
(2)![]() ,等式两端同时除以
,等式两端同时除以![]() 得:
得:![]() ,即
,即![]() ,
,
故![]() 是以
是以![]() 为首项,公差为
为首项,公差为![]() 的等差数列,通项公式为
的等差数列,通项公式为![]() ,
,
则![]() .
.
因为当![]() ,
,![]() ,当
,当![]() 时
时![]() ,
,![]() ,所以当
,所以当![]() 或
或![]() 时,
时,![]() 取最大值,对任意
取最大值,对任意![]() ,
,![]() 恒成立.
恒成立.
(3)由题意,![]() ,
,
则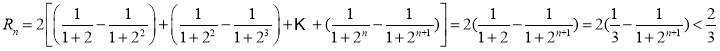 ,故
,故![]() .
.
所以![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目