题目内容
、(满分17分)
设数列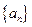 的前
的前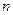 项和为
项和为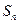 ,对任意的正整数
,对任意的正整数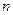 ,都有
,都有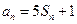 成立,记
成立,记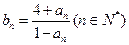 。
。
(I)求数列 的通项公式;
的通项公式;
(II)记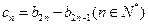 ,设数列
,设数列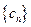 的前
的前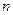 项和为
项和为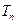 ,求证:对任意正整数
,求证:对任意正整数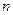 都有
都有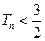 ;
;
设数列
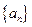 的前
的前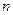 项和为
项和为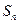 ,对任意的正整数
,对任意的正整数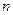 ,都有
,都有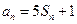 成立,记
成立,记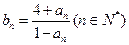 。
。(I)求数列
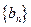 的通项公式;
的通项公式;(II)记
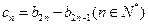 ,设数列
,设数列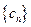 的前
的前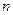 项和为
项和为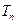 ,求证:对任意正整数
,求证:对任意正整数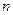 都有
都有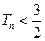 ;
;(Ⅰ)当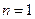 时,
时,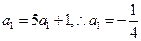 ……………………………1分
……………………………1分
又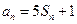 ,则
,则 ,将两式相减得:
,将两式相减得:
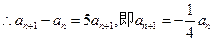 ……………………………3分
……………………………3分
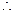 数列
数列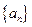 成等比数列,其首项
成等比数列,其首项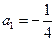 ,公比是
,公比是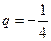 ……………………………4分
……………………………4分
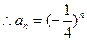 ……………………………5分
……………………………5分
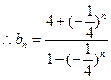 ……………………………6分
……………………………6分
(Ⅱ)由(Ⅰ)知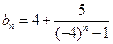 .
. 

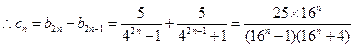
=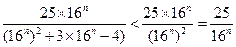 ……………………………9分
……………………………9分
又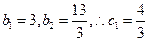
当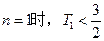 ……………………………11分
……………………………11分
当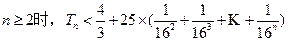 ……………………………13分
……………………………13分
 =" "
=" " 
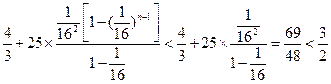 ……………………………17分
……………………………17分
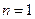 时,
时,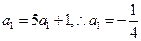 ……………………………1分
……………………………1分又
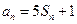 ,则
,则 ,将两式相减得:
,将两式相减得: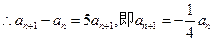 ……………………………3分
……………………………3分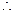 数列
数列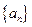 成等比数列,其首项
成等比数列,其首项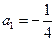 ,公比是
,公比是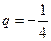 ……………………………4分
……………………………4分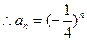 ……………………………5分
……………………………5分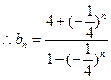 ……………………………6分
……………………………6分(Ⅱ)由(Ⅰ)知
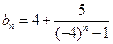 .
. 

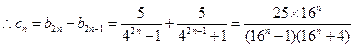
=
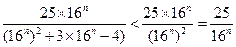 ……………………………9分
……………………………9分又
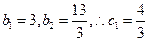
当
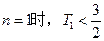 ……………………………11分
……………………………11分当
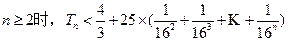 ……………………………13分
……………………………13分 =" "
=" " 
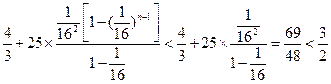 ……………………………17分
……………………………17分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
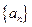
 的前
的前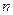 项和为
项和为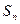 ,等比数列
,等比数列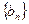 的前
的前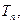 已知数列
已知数列
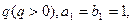
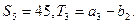
 )求数列
)求数列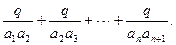

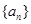 中,
中,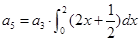 ,则
,则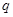 = ( )
= ( )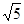
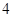
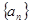 中,
中,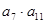 =6,
=6,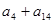 =5,则
=5,则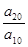 等于( )
等于( )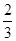
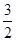

 个等式为
个等式为  满足
满足 ,且对任意的正整数
,且对任意的正整数 都有
都有 ,若数列
,若数列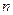 项和为
项和为 ,则
,则 满足
满足 ,则
,则 =( )
=( )


 是公差为-2的等差数列,如果
是公差为-2的等差数列,如果 ,那么
,那么 ( )
( )  B.
B. 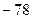 C
C 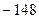 D.
D. 
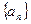 是等差数列,前n项和为Sn,
是等差数列,前n项和为Sn,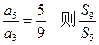 =
=