题目内容
((本题满分12分)
已知椭圆方程为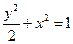 ,斜率为
,斜率为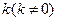 的直线
的直线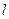 过椭圆的上焦点且与椭圆相交于
过椭圆的上焦点且与椭圆相交于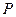 ,
,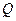 两点,线段
两点,线段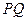 的垂直平分线与
的垂直平分线与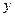 轴相交于点
轴相交于点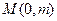 .
.
(Ⅰ)求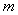 的取值范围;
的取值范围;
(Ⅱ)求△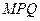 面积的最大值.
面积的最大值.
已知椭圆方程为
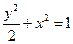 ,斜率为
,斜率为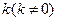 的直线
的直线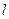 过椭圆的上焦点且与椭圆相交于
过椭圆的上焦点且与椭圆相交于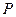 ,
,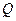 两点,线段
两点,线段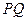 的垂直平分线与
的垂直平分线与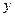 轴相交于点
轴相交于点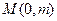 .
.(Ⅰ)求
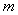 的取值范围;
的取值范围;(Ⅱ)求△
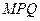 面积的最大值.
面积的最大值.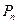 解:(Ⅰ)设直线
解:(Ⅰ)设直线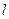 的方程为
的方程为 ,由
,由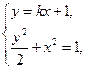 可得
可得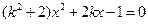 .
.
设
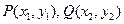 ,则
,则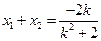 ,
,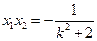 .
.可得
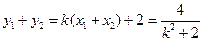 .……………………………………3分
.……………………………………3分设线段
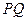 中点为
中点为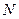 ,则点
,则点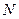 的坐标为
的坐标为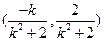 ,
,由题意有
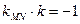 ,可得
,可得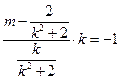 .可得
.可得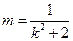 ,
,又
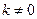 ,所以
,所以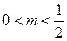 .………………………………6分
.………………………………6分(Ⅱ)设椭圆上焦点为
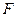 ,
,则
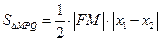
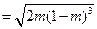 ……………………………9分
……………………………9分所以△
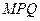 的面积为
的面积为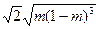 (
(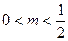 ).
).设
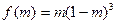 ,则
,则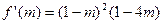 .
.可知
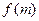 在区间
在区间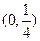 单调递增,在区间
单调递增,在区间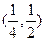 单调递减.
单调递减.所以,当
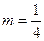 时,
时,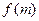 有最大值
有最大值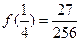 .
.所以,当
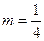 时,△
时,△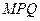 的面积有最大值
的面积有最大值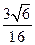 .………………………………12
.………………………………12略

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
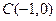 及椭圆
及椭圆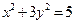 ,过点
,过点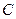 的动直线与椭圆相交于
的动直线与椭圆相交于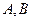 两点.
两点.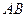 中点的横坐标是
中点的横坐标是 ,求直线
,求直线 2)在
2)在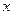 轴上是否存在点
轴上是否存在点 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点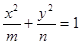 的离心率为_______________
的离心率为_______________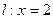 ,设动点P到直线
,设动点P到直线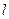 的距离为
的距离为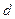 ,已知
,已知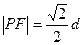 ,且
,且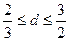 .
.
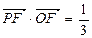 ,求向量
,求向量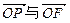 的夹角;
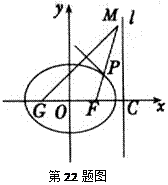
的夹角;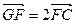 ,点M满足
,点M满足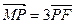 ,且线段MG的垂直平分线经过点P,求
,且线段MG的垂直平分线经过点P,求 的面积.
的面积.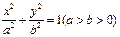 中心的直线与椭圆交于A、B两点,右焦点为F2,则△ABF2
中心的直线与椭圆交于A、B两点,右焦点为F2,则△ABF2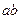 B.
B.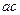 C.
C.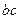 D.
D.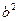
 :
: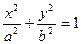 ,以抛物线
,以抛物线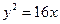 的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为
的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为  A.
A. B.
B. 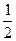 C.
C. 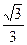 D.
D. 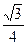
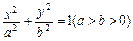 短轴端点为A,B.点P是椭圆上除A,B外任意一点,则直线PA,PB的斜率之积为 .
短轴端点为A,B.点P是椭圆上除A,B外任意一点,则直线PA,PB的斜率之积为 .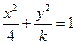 的离心率
的离心率 ,则
,则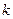 的取值范围是 ( )
的取值范围是 ( )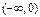
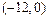
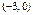

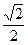
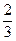 ≤e<1
≤e<1